Bài 2: Đồ thị độ dịch chuyển theo thời gian. Độ dịch chuyển tổng hợp và vận tốc tổng hợp
Nội dung lý thuyết
I. Đồ thị độ dịch chuyển - thời gian trong chuyển động thẳng
Trong chuyển động thẳng đều thì d = v.t (với v là một hẳng số). Biểu thức d = v.t có dạng giống biểu thức của hàm số y = a.x có đường biểu diễn là một đoạn thẳng.

Hình 1: Đồ thị hàm số y = a.x (a > 0)
Khi vật chuyển động thẳng với vận tốc không đổi v > 0 thì d = v.t. Phương trình này có dạng của hàm số y = ax nên có đồ thị ở Hình 1.
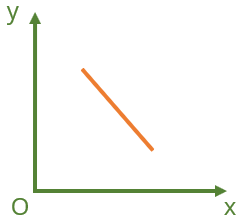
Hình 2: Đồ thị hàm số y = a.x + b (a < 0; b > 0)
Khi vật đang chuyển động thẳng, theo chiều dương, nếu đổi chiều chuyển động thì trong khoảng thời gian chuyển động ngược chiều đó, quãng đường đi được vẫn có giá trị dương còn độ dịch chuyển có giá trị âm. Đồ thị độ dịch chuyển – thời gian có dạng như Hình 2.
@2569224@
Vận tốc có giá trị bằng hệ số góc (độ dốc) của đường biểu diễn trong đồ thị độ dịch chuyển – thời gian của chuyển động thẳng.
II. Độ dịch chuyển tổng hợp – vận tốc tổng hợp

Một phụ xe đi từ cuối lên đầu của một xe bus khi xe đang chuyển động. Để xem xét độ dịch chuyển của người phụ xe, ta quy ước:
+ Vật số 1 (người) là vật chuyển động đang xét.
+ Vật số 2 (xe bus) là vật chuyển động được chọn làm gốc của hệ quy chiếu chuyển động.
+ Vật số 3 (đường) là vật đứng yên được chọn làm gốc của hệ quy chiếu đứng yên.
Khi vật 1 có độ dịch chuyển \(\overrightarrow{d_{12}}\) trong hệ quy chiếu chuyển động, đồng thời hệ quy chiếu chuyển động cũng có độ dịch chuyển \(\overrightarrow{d_{23}}\) so với hệ quy chiếu đứng yên. Độ dịch chuyển tổng hợp khi đó là:
\(\overrightarrow{d_{13}}=\overrightarrow{d_{12}}+\overrightarrow{d_{23}}\)
@2569284@
Xét trong khoảng thời gian ∆t rất nhỏ kết hợp với định nghĩa của vận tốc, ta suy ra biểu thức của vận tốc tổng hợp:
\(\overrightarrow{\text{v}_{13}}=\overrightarrow{\text{v}_{12}}+\overrightarrow{\text{v}_{23}}\)
Kết luận: Vận tốc tuyệt đối (vận tốc của vật đối với hệ quy chiếu đứng yên) bằng tổng vận tốc tương đối (vận tốc của vật đối với hệ quy chiếu chuyển động) và vận tốc kéo theo (vận tốc của hệ quy chiếu chuyển động đối với hệ quy chiếu đứng yên).
1. Vận tốc có giá trị bằng hệ số góc (độ dốc) của đường biểu diễn trong đồ thị độ dịch chuyển – thời gian của chuyển động thẳng.
2. Công thức cộng vận tốc: \(\overrightarrow{\text{v}_{13}}=\overrightarrow{\text{v}_{12}}+\overrightarrow{\text{v}_{23}}\)