Bài 17: Dấu của tam thức bậc hai
Các câu hỏi tương tự
Cho hàm số bậc hai y f(x) {x^2} - 4x + 3a) Xác định hệ số a. Tính f(0);f(1);f(2);f(3);f(4) và nhận xét về dấu của chúng so với dấu của hệ số ab) Cho đồ thị hàm số yf(x) (H.6.17). Xét từng khoảng left( { - infty ;1} right);left( {1;3} right);left( {3; + infty } right), đồ thị nằm phía trên hay phía dưới trục Ox?c) Nhận xét về dấu của f(x) và dấu của hệ số a trên từng khoảng đó.
Đọc tiếp
Cho hàm số bậc hai \(y = f(x) = {x^2} - 4x + 3\)
a) Xác định hệ số a. Tính \(f(0);f(1);f(2);f(3);f(4)\) và nhận xét về dấu của chúng so với dấu của hệ số a
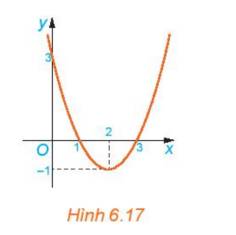
b) Cho đồ thị hàm số y=f(x) (H.6.17). Xét từng khoảng \(\left( { - \infty ;1} \right);\left( {1;3} \right);\left( {3; + \infty } \right)\), đồ thị nằm phía trên hay phía dưới trục Ox?
c) Nhận xét về dấu của f(x) và dấu của hệ số a trên từng khoảng đó.
Xét dấu các tam thức bậc hai sau:
a) \( - 3{x^2} + x - \sqrt 2 \)
b) \({x^2} + 8x + 16\)
c) \( - 2{x^2} + 7x - 3\)
Xét dấu các tam thức bậc hai sau:
a) \(3{x^2} - 4x + 1\)
b) \({x^2} + 2x + 1\)
c) \( - {x^2} + 3x - 2\)
d) \( - {x^2} + x - 1\)
Giải các bất phương trình sau:
a) \( - 5{x^2} + x - 1 \le 0\)
b) \({x^2} - 8x + 16 \le 0\)
c) \({x^2} - x + 6 > 0\)
Giải các bất phương trình bậc hai:
a) \({x^2} - 1 \ge 0\)
b) \({x^2} - 2x - 1 < 0\)
c) \( - 3{x^2} + 12x + 1 \le 0\)
d) \(5{x^2} + x + 1 \ge 0\)
Hãy cho biết biểu thức nào sau đây là tam thức bậc hai.
\(A = 3x + 2\sqrt x + 1\)
\(B = - 5{x^4} - 3{x^2} + 4\)
\(C = - \frac{2}{3}{x^2} + 7x - 4\)
\(D = {\left( {\frac{1}{x}} \right)^2} + 2.\frac{1}{x} + 3\)
Hãy chỉ ra một đặc điểm chung của các biểu thức dưới đây:
\(A = 0,5{x^2}\)
\(B = 1 - {x^2}\)
\(C = {x^2} + x + 1\)
\(D = (1 - x)(2x + 1)\)
Tìm các giá trị của tham số m để tam thức bậc hai sau dương với mọi \(x \in \mathbb{R}\):
\({x^2} + (m + 1)x + 2m + 3\)
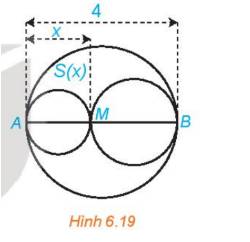
Xét đường tròn đường kính AB4 và một điểm M di chuyển trên đoạn AB, đặt AMx (H.6.19). Xét hai đường tròn đường kính AM và MB. Kí hiệu S(x) là diện tích phần hình phằng nằm trong hình tròn lớn và nằm ngoài hai hình tròn nhỏ. Xác định các giá trị của x để diện tích S(x) không vượt quá một nửa tổng diện tích hai hình tròn nhỏ.
Đọc tiếp
Xét đường tròn đường kính AB=4 và một điểm M di chuyển trên đoạn AB, đặt AM=x (H.6.19). Xét hai đường tròn đường kính AM và MB. Kí hiệu S(x) là diện tích phần hình phằng nằm trong hình tròn lớn và nằm ngoài hai hình tròn nhỏ. Xác định các giá trị của x để diện tích S(x) không vượt quá một nửa tổng diện tích hai hình tròn nhỏ.