Gọi t là nhiệt độ của nước trong bình sau khi thả vật thứ hai vào.
\(q_v\) là nhiệt dung của vật, \(q_v=c_v.m_v\)
\(q_n\) là nhiệt dung của nước trong bình, \(q_n=c_n.m_n\)
Khi thả vật thứ nhất vào:
pt cân bằng nhiệt:
\(q_v.\left(120-40\right)=q_n\left(40-20\right)\)
\(\Leftrightarrow q_n=4q_n\)
Khi thả vật thứ hai vào:
\(q_v\left(100-t\right)=q_n.\left(t-40\right)\)
\(\Leftrightarrow100-t=5t-200\)
\(\Leftrightarrow6t=300\)
\(\Leftrightarrow t=50^0\)
Vậy sau khi thả vật thứ hai vào thì nước trong bình sẽ tăng
tại sao lại thành 5t, lẽ ra phải 4t chứ
Gọi to là nhiệt độ ban đầu của nước và bình; t1 và t2 là nhiệt độ của nước và binhg sau khi thả vật thứ nhất và thứ hai vào bình; tv1, tv2 là nhiệt độ của vật thứ nhất và thứ hai khi thả vào nước. Ta có:
Lần thứ nhất:
+ Trước khi thả: vật (mv,cv,tv1); bình (mb,cb,t0); nước (m,c,t0)
+ Sau khi thả: vật ((mv,cv,t1); bình (mb,cb,t1); nước (m,c,t1)
+ Phương trình cân bằng nhiệt: mvcv(tv1-t1)=mbcb(t1-t0)+mc(t1-t0)
Hay mvcv(tv1-t1)= (mbcb+mc)(t1-t0) (1)
Lần thả thứ hai:
+ Trước khi thả: vật (mv,cv,tv2); bình (mb,cb,t1); nước (m,c,t1)
+ Sau khi thả: vật ((mv,cv,t2); bình (mb,cb,t2); nước (m,c,t2)
+ Phương trình cân bằng nhiệt: mvcv(tv2-t2)=mbcb(t2-t1)+mc(t2-t1)+ mvcv(t2-t1)
Hay mvcv(tv2-t2)= (mbcb+mc+ mvcv)(t2-t1)
mvcv(tv2+t1-2t2)=( mbcb+mc)(t2-t1) (2)
Từ (1) và (2) suy ra:
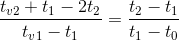
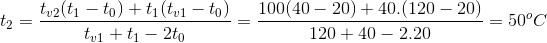






![Quen Sao [Shino Slimer]](https://hoc24.vn/images/avt/avt153636508_256by256.jpg)






