`a_1=0(cm//s^2); v_1=20(cm//s)`
`a_2 =40\sqrt{3}(cm//s^2);v_2=10(cm//s)`
Ta có: `\omega=\sqrt{[a_2 ^2-a_1 ^2]/[v_1 ^2-v_2 ^2]}`
`=4(rad//s)`
Mà `v_[max]=A.\omega=20(cm//s)`
`=>A=20/4=5(cm)`.
`a_1=0(cm//s^2); v_1=20(cm//s)`
`a_2 =40\sqrt{3}(cm//s^2);v_2=10(cm//s)`
Ta có: `\omega=\sqrt{[a_2 ^2-a_1 ^2]/[v_1 ^2-v_2 ^2]}`
`=4(rad//s)`
Mà `v_[max]=A.\omega=20(cm//s)`
`=>A=20/4=5(cm)`.
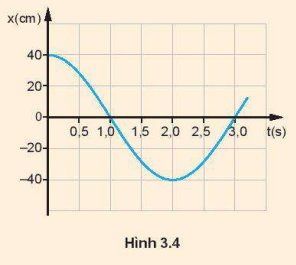
Hình 3.4 là đồ thị li độ – thời gian của một vật dao động điều hoà. Sử dụng đô thị để tính các đại lượng sau:
a) Tốc độ của vật ở thời điểm t = 0 s.
b) Tốc độ cực đại của vật.
c) Gia tốc của vật tại thời điểm t = 1,0 s
Phương trình dao động của một vật là x = 5cos4πt (cm). Hãy viết phương trình vận tốc, gia tốc và vẽ đồ thị li độ, vận tốc, gia tốc theo thời gian của vật.
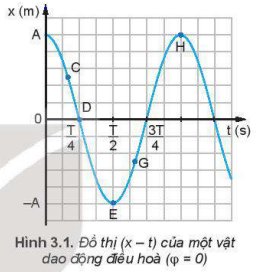
Ta có thể dựa vào đồ thị (x – t) của dao động điều hòa để xác định vận tốc và gia tốc của vật được không?
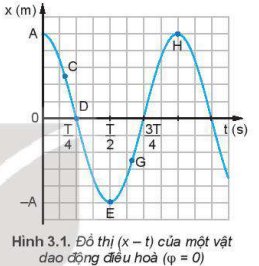
Đặt một loại thước kẻ (20 cm) cho mép của thước tiếp xúc với đồ thị li độ - thời gian (Hình 3.1) ở một số điểm C, D, E, G, H. Từ độ dốc của thước hãy so sánh độ lớn vận tốc của vật tại các điểm C, E, H.
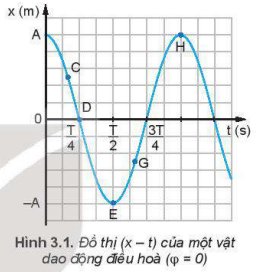
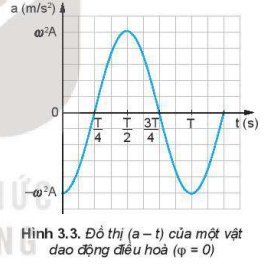
So sánh đồ thị Hình 3.3 và Hình 3.1 ta có nhận xét gì về pha của li độ và gia tốc của một dao động.
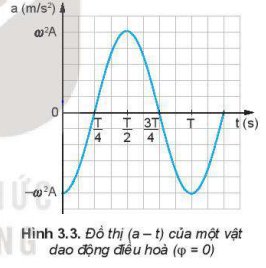
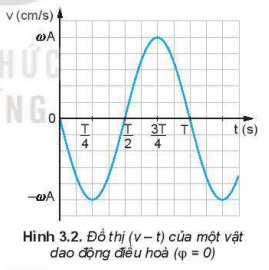
Dùng thước kẻ (loại 20 cm) để xác định xem trên đồ thị (v – t) Hình 3.2, tại thời điểm nào độ dốc của đồ thị bằng 0 và tại thời điểm nào độ dốc của đồ thị cực đại. Từ đó, so sánh độ lớn của gia tốc trên đô thị (a – t) Hình 3.3 ở các thời điểm tương ứng.
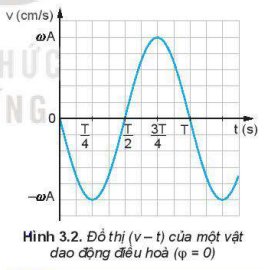
Trong các khoảng thời gian từ 0 đến \(\dfrac{T}{4}\), từ \(\dfrac{T}{4}\) đến \(\dfrac{T}{2}\), từ \(\dfrac{T}{2}\) đến \(\dfrac{3T}{4}\), từ \(\dfrac{3T}{4}\) đến \(T\), vận tốc của dao động điều hoà thay đổi như thế nào?
Trong các khoảng thời gian từ 0 đến \(\dfrac{T}{4}\), từ \(\dfrac{T}{4}\) đến \(\dfrac{T}{2}\), từ \(\dfrac{T}{2}\) đến \(\dfrac{3T}{4}\), từ \(\dfrac{3T}{4}\) đến \(T\), gia tốc của dao động thay đổi như thế nào?
So sánh đồ thị của vận tốc (Hình 3.2) với đồ thị của li độ (Hình 3.1), hãy cho biết vận tốc sớm pha hay trễ pha bao nhiêu so với li độ.