Một trường trung học có sở có 600 học sinh. Tỉ lệ phần trăm học sinh mỗi khối được cho bởi biểu đồ trong Hình 4. Chọn ngẫu nhiên một học sinh trong trường để dự phỏng vấn. Biết rằng mọi học sinh của trường đều có khả năng được lựa chọn như nhau.
a) Tính xác suất của biến cố “Học sinh được chọn thuộc khối 9”.
b) Tính xác suất của biến cố “Học sinh được chọn không thuộc khối 6”.
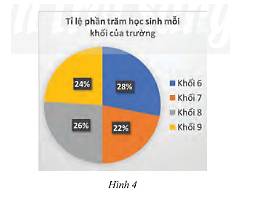
Số học sinh khối 6 là:
\(600.28\% = 168\) (học sinh)
Số học sinh khối 7 là:
\(600.22\% = 132\) (học sinh)
Số học sinh khối 8 là:
\(600.25\% = 150\) (học sinh)
Số học sinh khối 6 là:
\(600.24\% = 144\) (học sinh)
a) Gọi \(A\) là biến cố: “Học sinh được chọn thuộc khối 9”.
Biến cố \(A\) xảy ra khi bạn học sinh chọn được là học sinh khối 9.
Xác suất của biến có \(A\) là:
\(P\left( A \right) = \frac{{144}}{{600}} = \frac{6}{{25}}\)
b) Gọi \(B\) là biến cố: “Học sinh được chọn không thuộc khối 6”.
Biến cố \(B\) xảy ra khi bạn học sinh chọn được là học sinh khối 7, khối 8, khối 9.
Tổng số học sinh khối 7, khối 8 và khối 9 là:
\(12 + 150 + 144 = 426\) (học sinh)
Xác suất của biến có \(B\) là:
\(P\left( B \right) = \frac{{426}}{{600}} = \frac{{71}}{{100}}\).