Ôn tập chương Hình trụ, Hình nón, Hình cầu
Các câu hỏi tương tự
Với nửa hình cầu bán kính r và một hình trụ có bán kính đường tròn đáy và chiều cao đều bằng h
a) Khi r = 12 (cm) và thể tích hai hình bằng nhau thì giá trị h(cm) làm tròn đến chữ số thập phân thứ nhất là bao nhiêu ?
b) Khi h = 12 (cm) và tổng diện tích nửa mặt cầu và diện tích "hình tròn đáy" gấp ba lần diện tích toàn phần của hình trụ thì r (cm) bằng bao nhiêu ?
Cho hình vuông ABCD nội tiếp đường tròn tâm O, bán kính R và GEF là tam giác đều nội tiếp đường tròn đó, EF là dây song song với AB (h. 119). Cho hình đó quay xung quanh trục GO. Chứng minh rằng:
a) Bình phương thể tích của hình trụ sinh ra bởi hình vuông bằng tích của thể tích hình cầu sinh ra bởi hình tròn và thể tích hình nón do tam giác đều sinh ra.
b) Bình phương diện tích toàn phần của hình trụ bằng tích của diện tích hình cầu và diện tích toàn phần của hình nón.
Đọc tiếp
Cho hình vuông ABCD nội tiếp đường tròn tâm O, bán kính R và GEF là tam giác đều nội tiếp đường tròn đó, EF là dây song song với AB (h. 119). Cho hình đó quay xung quanh trục GO. Chứng minh rằng:
a) Bình phương thể tích của hình trụ sinh ra bởi hình vuông bằng tích của thể tích hình cầu sinh ra bởi hình tròn và thể tích hình nón do tam giác đều sinh ra.
b) Bình phương diện tích toàn phần của hình trụ bằng tích của diện tích hình cầu và diện tích toàn phần của hình nón.
-0132.jpg)
Với một hình nón có bán kính đường tròn đáy là r (cm) và chiều cao 2r (cm) và một hình cầu bán kính r (cm). Hãy tính :
a) Diện tích mặt cầu, biết diện tích toàn phần của hình nón là \(21,06cm^2\)
b) Thể tích hình nón, biết thể tích hình cầu là \(15,8cm^3\)
Có một chai đựng nước suối, bạn An đo đường kính của đáy chai bằng 6 cm, đo chiều cao của phần nước trong chia được 9 cm rồi lật ngược chai và đo chiều cao của phần hình trụ không chứa nước được 7 cm.
a) Tính thể tích lượng nước trong chai
b) Tính thể tích chai
Một hình chữ nhật ABCD có AB > AD, diện tích và chu vi của nó theo thứ tự là 2a2 và 6a. Cho hình vẽ quay xung quanh cạnh AB, ta được một hình trụ.
Tính diện tích xung quanh và thể tích của hình trụ này.
một khối gỗ hình trụ có chiều cao gấp 3 lần đường kính đáy biết diện tích toàn phần của khối gỗ là 7 pi . tính thể tích
Cho ba điểm A, O, B thẳng hàng theo thứ tự đó, OA a; OB b (a, b cùng đơn vị cm).
Qua A và B vẽ theo thứ tự các tia Ax và By cùng vuông góc với AB và cùng phía với AB. Qua O vẽ hai tia vuông góc với nhau và cắt Ax ở C, By ở D (xem hình 116).
a) Chứng minh AOC và BDO là hai tam giác đồng dạng; từ đó suy ra tích AC.BD không đổi.
b) Tính diện tích hình thang ABDC khi widehat{COA}60^o.
c) Với widehat{COA}60^o cho hình vẽ quay xung quanh AB. Hãy tính tỉ số thể tích với các hình do các tam giác A...
Đọc tiếp
Cho ba điểm A, O, B thẳng hàng theo thứ tự đó, OA = a; OB = b (a, b cùng đơn vị cm).
Qua A và B vẽ theo thứ tự các tia Ax và By cùng vuông góc với AB và cùng phía với AB. Qua O vẽ hai tia vuông góc với nhau và cắt Ax ở C, By ở D (xem hình 116).
a) Chứng minh AOC và BDO là hai tam giác đồng dạng; từ đó suy ra tích AC.BD không đổi.
b) Tính diện tích hình thang ABDC khi \(\widehat{COA}=60^o.\)
c) Với \(\widehat{COA}=60^o\) cho hình vẽ quay xung quanh AB. Hãy tính tỉ số thể tích với các hình do các tam giác AOC và BOD tạo thành.
-0131.jpg)
Độ dài các cạnh của một tam giác ABC vuông tại A, thỏa mãn các hệ thức sau :
BCAB+2a
ACdfrac{1}{2}left(BC+ABright)
a là một độ dài cho trước
a) Tính theo a, độ dài các cạnh và chiều cao AH của tam giác
b) Tam giác ABC nội tiếp được trong nửa hình tròn tâm O. Tính diện tích của phần thuộc nửa đường tròn nhưng ở ngoài tam giác ssos
c) Cho tam giác ABC quay một vòng quanh cạnh huyền BC. Tính tỉ số diện tích giữa các phần do các dây cung AB và...
Đọc tiếp
Độ dài các cạnh của một tam giác ABC vuông tại A, thỏa mãn các hệ thức sau :
\(BC=AB+2a\)
\(AC=\dfrac{1}{2}\left(BC+AB\right)\)
a là một độ dài cho trước
a) Tính theo a, độ dài các cạnh và chiều cao AH của tam giác
b) Tam giác ABC nội tiếp được trong nửa hình tròn tâm O. Tính diện tích của phần thuộc nửa đường tròn nhưng ở ngoài tam giác ssos
c) Cho tam giác ABC quay một vòng quanh cạnh huyền BC. Tính tỉ số diện tích giữa các phần do các dây cung AB và AC tạo ra
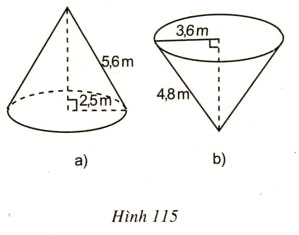
Hãy tính diện tích toàn phần của các hình tương ứng theo các kích thước đã cho trên hình 115.