BT3:
a) Xét \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\) ( định lí tổng ba góc trong một tam giác )
\(\Rightarrow\)\(\widehat{A}+60^0+\widehat{C}=180^0\)
\(\Rightarrow\)\(\widehat{A}+\widehat{C}=120^0\)
\(\Rightarrow2\widehat{OAC}+2\widehat{OCA}=120^0\)
\(\Rightarrow2\left(\widehat{OAC}+\widehat{OCA}\right)\)= 1200
\(\Rightarrow\widehat{OAC}+\widehat{OCA}=60^0\)
Xét \(\widehat{OAC}+\widehat{OCA}+\widehat{AOC}=180^0\) ( định lí tổng ba góc trong một tam giác )
\(\Rightarrow\widehat{AOC}=120^0\)
b) Có tia AO cắt BC tại M
\(\Rightarrow\widehat{BMC}=180^0\)
Lại có: \(\widehat{A}+\widehat{C}=120^0\) ( ở câu a)
\(\Rightarrow\widehat{C}< 120^0< 180^0\)
\(\Rightarrow\widehat{C}< \widehat{BMC}\)
BT3:
a) Xét \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\) (đlí tồng ba góc trong một tam giác )
\(\Rightarrow\widehat{C}=30^0\)
b) Có AD là phân giác góc A
\(\Rightarrow\widehat{CAD}=\widehat{DAB}=\dfrac{90^0}{2}=45^0\)
Xét \(\Delta HAB\) có \(\widehat{H}+\widehat{HAB}+\widehat{HBA}=180^0\) (đlí tồng ba góc trong một tam giác )
\(\Rightarrow\widehat{HAB}=180^0-90^0-60^0=30^0\)
Lại có: \(\widehat{CAD}+\widehat{DAH}+\widehat{HAB}=\widehat{A}=90^0\)
\(\Rightarrow45^0+30^0+\widehat{HAD}=90^0\)
\(\Rightarrow\widehat{HAD}=15^0\)
BT5:
a) Xét \(\Delta ABC\) có \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\) (đlí tổng ba góc trong một tam giác )
\(\Rightarrow\widehat{ACB}=180^0-90^0-30^0=60^0\)
b) Có CD là tia phân giác góc C
\(\Rightarrow\widehat{DCB}=\dfrac{\widehat{C}}{2}=\dfrac{60^0}{2}=30^0\)
Xét \(\Delta DCB\) có \(\widehat{D}+\widehat{C}+\widehat{B}=180^0\)(đlí tổng ba góc trong một tam giác )
\(\Rightarrow\widehat{BDC}=180^0-30^0-30^0=120^0\)
BT6:
a) Xét \(\Delta ACE\) có \(\widehat{A}+\widehat{ACE}+\widehat{AEC}=180^0\)(đlí tổng ba góc trong một tam giác )
\(\Rightarrow80^0+90^0+\widehat{ACE}=180^0\)
\(\Rightarrow\widehat{ACE}=10^0\)
b) Xét \(\Delta BEF\) có \(\widehat{BEF}+\widehat{EBF}+\widehat{BFE}=180^0\) (đlí tổng ba góc trong một tam giác )
Xét \(\Delta FDC\) có \(\widehat{D}+\widehat{C}+\widehat{F}=180^0\)(đlí tổng ba góc trong một tam giác )
Có: \(\widehat{E}=\widehat{D}=90^0\)
\(\widehat{BFE}=\widehat{DFC}\) ( đối đỉnh)
\(\Rightarrow\widehat{EBF}=\widehat{DCF}\)

 Mong các bạn và thầy cô giáo trên hoc24h giúp mk giả bài 3,4,5,6 trong đề. Cảm ơn mn nhé! 😊😀😁
Mong các bạn và thầy cô giáo trên hoc24h giúp mk giả bài 3,4,5,6 trong đề. Cảm ơn mn nhé! 😊😀😁




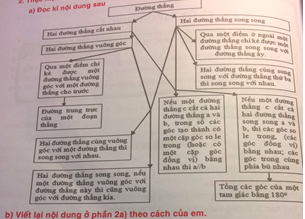






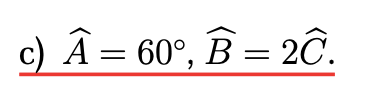

 Giúp mình cái bài định lí 2 nha?!!! cảm ơn mn!!!!
Giúp mình cái bài định lí 2 nha?!!! cảm ơn mn!!!!