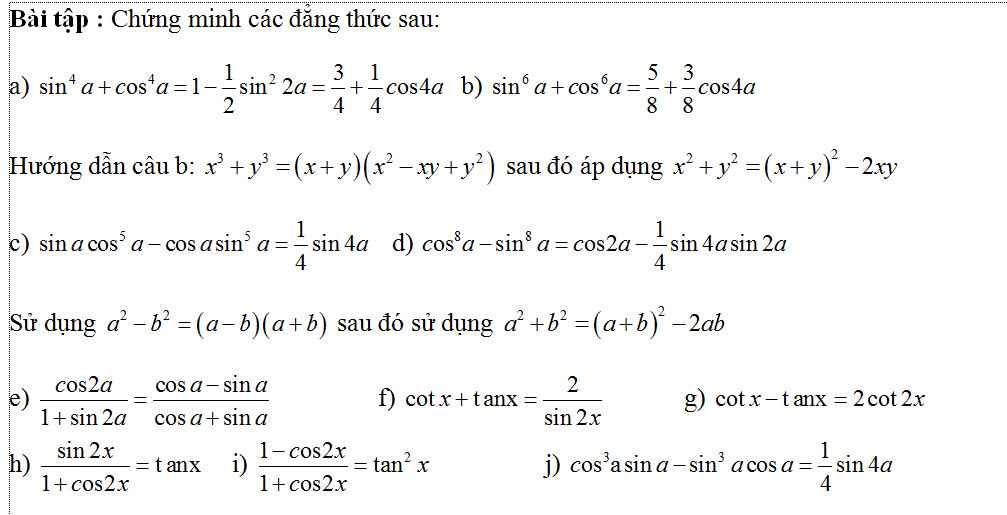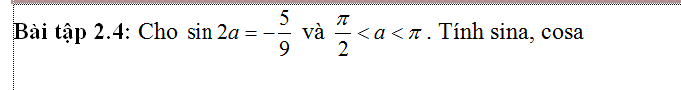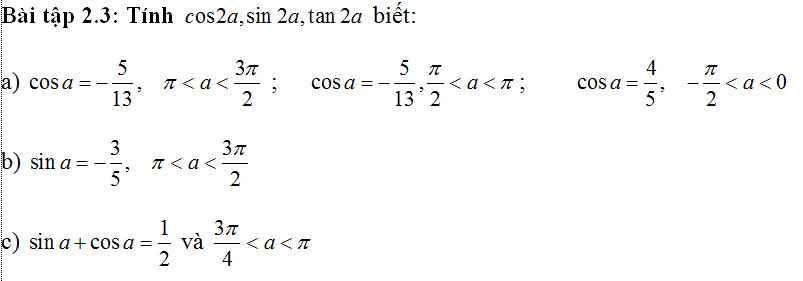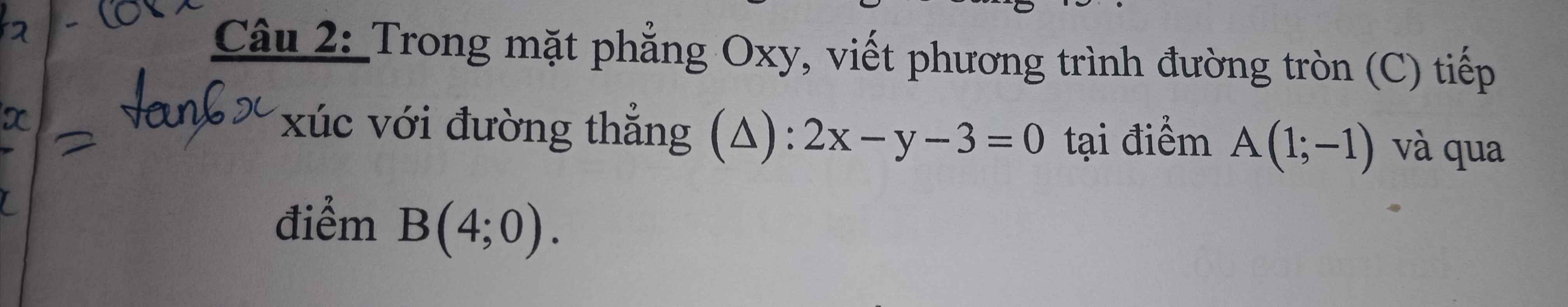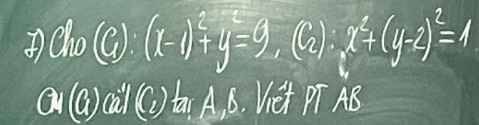Từ pt (E) ta xác định được: \(a=5;b=3;c=4\)
\(F_1F_2=2c=8\Rightarrow\) chu vi tam giác \(MF_1F_2=MF_1+MF_2+F_1F_2=2a+2c=18\)
\(\Rightarrow\) nửa chu vi \(p=9\)
Tam giác \(MF_1F_2\) vuông tại M \(\Rightarrow OM=\dfrac{1}{2}F_1F_2=4\)
Gọi \(M\left(x;y\right)\Rightarrow\overrightarrow{OM}=\left(x;y\right)\Rightarrow OM^2=x^2+y^2=16\)
\(\Rightarrow x^2=16-y^2\)
Thay vào pt (E):
\(\dfrac{16-y^2}{25}+\dfrac{y^2}{9}=1\Rightarrow y^2=\dfrac{81}{16}\Rightarrow\left|y\right|=\dfrac{9}{4}\)
\(S_{MF_1F_2}=\dfrac{1}{2}F_1F_2.d\left(M;F_1F_2\right)=\dfrac{1}{2}.2c.\left|y\right|=9\)
\(\Rightarrow r=\dfrac{S_{MF_1F_2}}{p}=1\)