§1. Cung và góc lượng giác
Các câu hỏi tương tự
Rút gọn biểu thức :
P= \(\dfrac{cos\left(\dfrac{\pi}{2}-2x\right)+sinx}{sinx+sin2x+sin3x}\)
Giải chi tiết mấy câu này giúp mình với ạ ( ét o ét cíuuuu ;-;)
Giải chi tiết mấy câu này giúp mình với ạ ( ét o ét cíuuuu ;-;)
Giải chi tiết mấy câu này giúp mình với ạ ( ét o ét cíuuuu ;-;)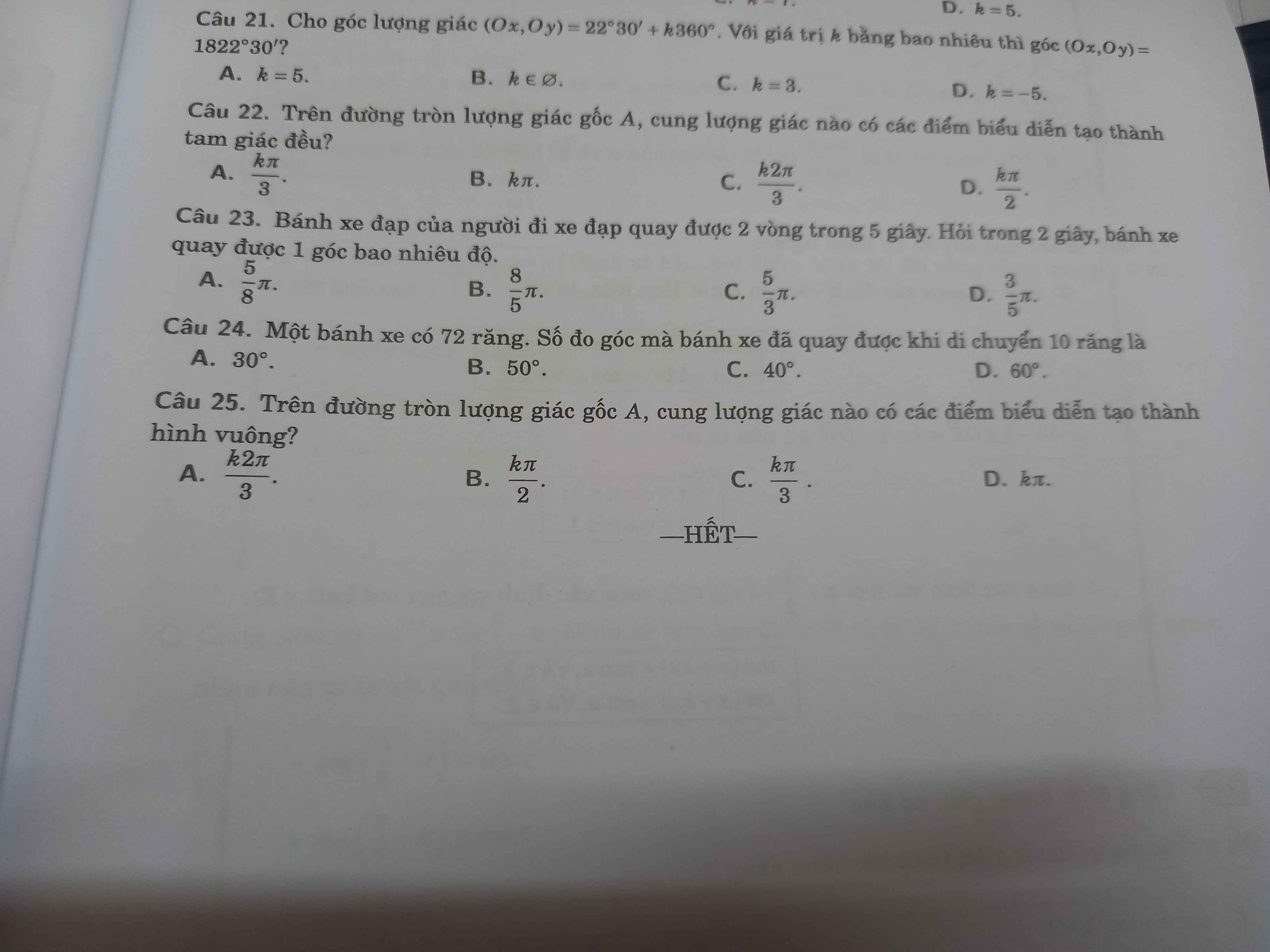
1. Rút gọn biểu thức sau: C sin6xtimes cot3x-cos6x
2. Chứng minh các đẳng thức sau:
a) sqrt{2}sinleft(x-frac{pi}{4}right)sqrt{2}cosleft(x+frac{pi}{4}right)
b) frac{cosleft(a+bright)times cosleft(a-bright)}{sin^2a+sin^2b}cot^2atimes cot^2b-1
3. Cho Delta ABC. Chứng minh rằng: sinfrac{A}{2}cosfrac{B}{2}times cosfrac{C}{2}-sinfrac{C}{2}times cosfrac{B}{2}
4. Chứng minh: Nếu sina2sinleft(a+bright) thì tanleft(a+bright)frac{sina}{cosb-2}
MONG MỌI NGƯỜI GIÚP ĐỠ CHO MÌNH! CẢM ƠN RẤT NHIỀU!
Đọc tiếp
1. Rút gọn biểu thức sau: C = \(sin6x\times cot3x-cos6x\)
2. Chứng minh các đẳng thức sau:
a) \(\sqrt{2}sin\left(x-\frac{\pi}{4}\right)=\sqrt{2}cos\left(x+\frac{\pi}{4}\right)\)
b) \(\frac{cos\left(a+b\right)\times cos\left(a-b\right)}{sin^2a+sin^2b}=cot^2a\times cot^2b-1\)
3. Cho \(\Delta ABC\). Chứng minh rằng: \(sin\frac{A}{2}=cos\frac{B}{2}\times cos\frac{C}{2}-sin\frac{C}{2}\times cos\frac{B}{2}\)
4. Chứng minh: Nếu \(sina=2sin\left(a+b\right)\) thì \(tan\left(a+b\right)=\frac{sina}{cosb-2}\)
MONG MỌI NGƯỜI GIÚP ĐỠ CHO MÌNH! CẢM ƠN RẤT NHIỀU!
Sao lại ra chỗ k2pi /6 v ạ, gthich giúp e vs ạ, e cảm ơn ạ 
cho mình hỏi câu này làm nào ạ... e yếu mấy cái này lắm
1-cot4x=2/sin2x-1/sin4x
cho tan -cos = 3. tính giá trị của biểu thức sau:
A= tan+cos
Khi biểu diễn các cung lượng giác có số đo khác nhau trên đường tròn lượng giác, có thể xảy ra trường hợp các điểm cuối của chúng trùng nhau không ? Khi nào trường hợp này xảy ra ?









