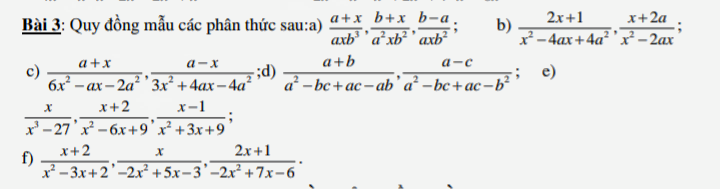\(a,\dfrac{a+x}{axb^3}=\dfrac{a\left(a+x\right)}{a^2xb^3};\dfrac{b+x}{a^2xb^2}=\dfrac{b\left(b+x\right)}{a^2xb^3};\dfrac{b-a}{axb^2}=\dfrac{ab\left(b-a\right)}{a^2xb^3}\\ b,\dfrac{2x+1}{x^2-4ax+4a^2}=\dfrac{x\left(2x+1\right)}{x\left(x-2a\right)^2};\dfrac{x+2a}{x^2-2ax}=\dfrac{\left(x+2a\right)\left(x-2a\right)}{x\left(x-2a\right)^2}\\ c,\dfrac{a+x}{6x^2-ax-2a^2}=\dfrac{a+x}{\left(3x-2a\right)\left(2x+a\right)}=\dfrac{\left(a+x\right)\left(x+2a\right)}{\left(3x-2a\right)\left(2x+a\right)}\\ \dfrac{a-x}{3x^2+4ax-4a^2}=\dfrac{a-x}{\left(3x-2a\right)\left(x+2a\right)}=\dfrac{\left(a-x\right)\left(2x+a\right)}{\left(3x-2a\right)\left(x+2a\right)\left(2x+a\right)}\)
Bài 4: Quy đồng mẫu thức nhiều phân thức
Đúng 1
Bình luận (0)
Các câu hỏi tương tự
Quy đồng mẫu 2 phân thức sau:
Mn ơi giúp em với ạ, 10h là em nộp bài rồi ạ!
Q: Quy đồng mẫu phân thức sau:
Mn chỉ em cách làm bài này với ạ!
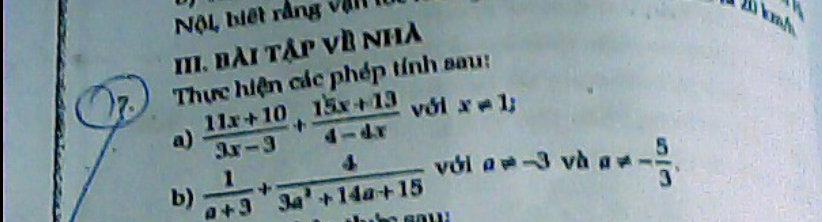
Mn giúp em với ạ
MN giúp em 2 câu này với: 1)11/x4y và 3/xy3 2)2/3x3y2 và 3/4x7y Em đang cần gấp ạ
giúp mình với nha mn ơi
Đọc tiếp
giúp mình với nha mn ơi
Mn giúp e với ạ
Quy đồng mẫu thức các phân thức sau:
x+5/x^2+6x+9; x+2/2x+6
Mn giúp e với ạ
Quy đồng mẫu thức các phân thức sau:
x+5/x^2+6x+9; x+2/2x+6
Mn giúp e với ạ
Quy đồng mẫu thức các phân thức sau:
3x/3x^3-27x; x+1/(x+2).(x+3)
Mn giúp e với ạ
Quy đồng mẫu thức các phân thức sau
\(\dfrac{4x^2-3x+8}{x^3-1};\dfrac{2x}{x^2+x+1};\dfrac{6}{1-x}\)