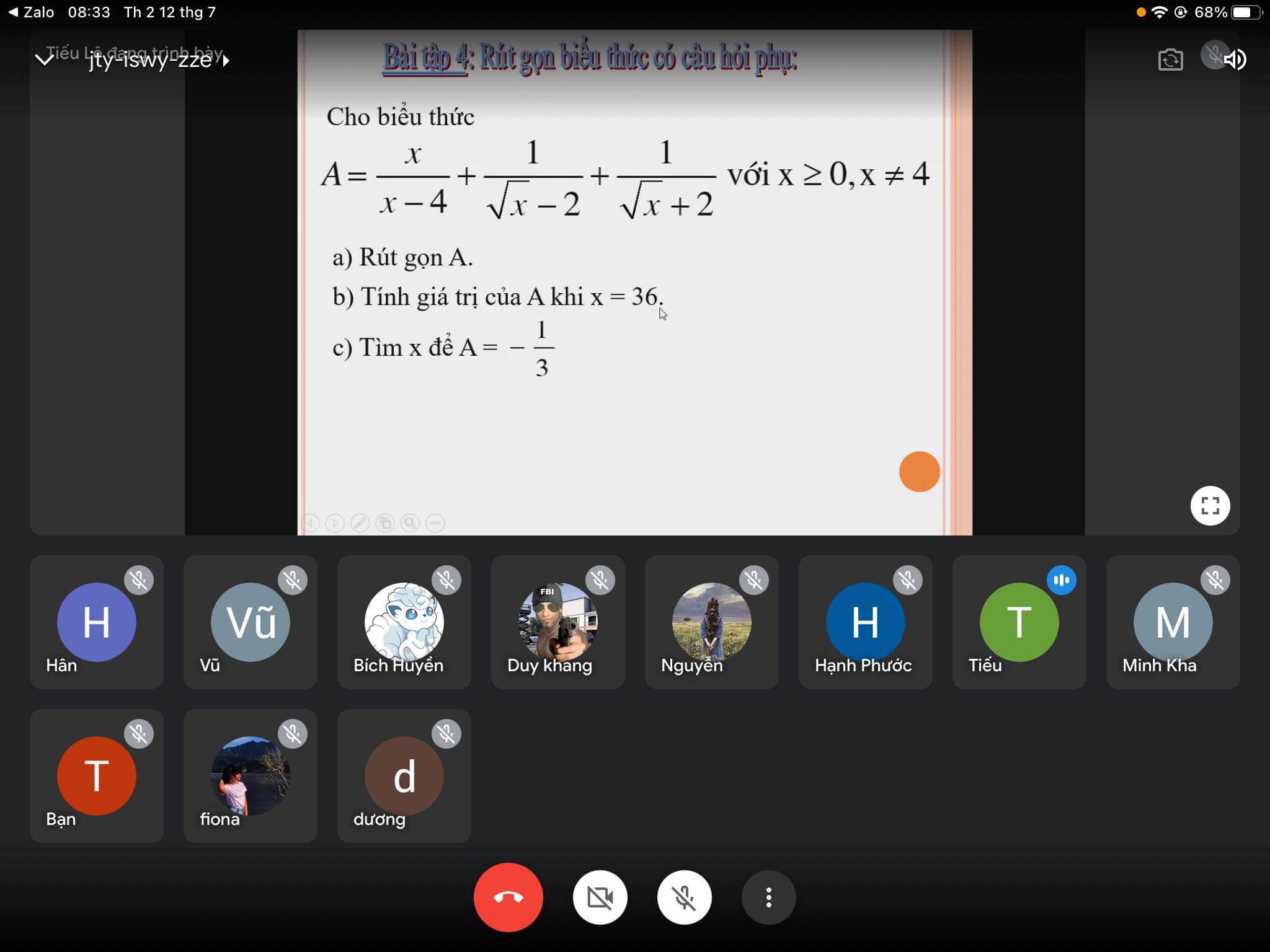
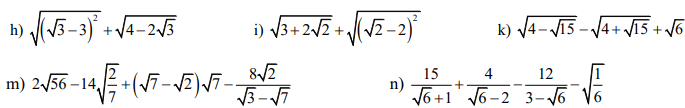Câu 6
a: Xét (O) có
DB,DC là tiếp tuyến
nên DB=DC
=>ΔDBC cân tại D
b: Xét (O) cos
ΔCABnội tiếp
AB là đường kính
=>ΔCAB vuông tại C
OB=OC
DB=DC
=>ODlà trung trực của BC
=>OD vuông góc với BC
mà AC vuông góc BC
nên OD//AC
d: Xét ΔCAB vuông tại C có
cos CAO=CA/CB=1/2
=>góc CAO=60 độ
=>ΔOAC đều
=>góc BOC=120 độ
=>góc BDC=60 độ
mà ΔBDC cân tại D
nên ΔBCD đều
\(CB=\sqrt{\left(2R\right)^2-R^2}=R\sqrt{3}\)
\(S_{BCD}=\left(R\sqrt{3}\right)^2\cdot\dfrac{\sqrt{3}}{4}=\dfrac{3\sqrt{3}\cdot R^2}{4}\)
Đúng 0
Bình luận (0)
