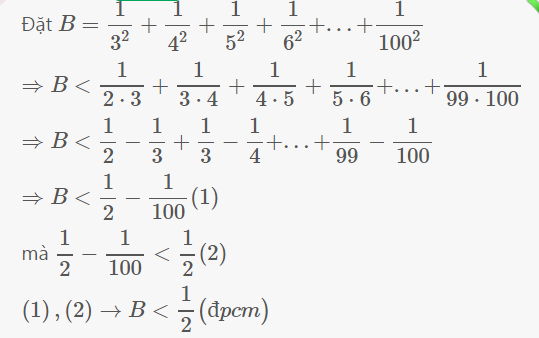Chương III : Phân số
Các câu hỏi tương tự
giải hộ mình nha
A=\(\frac{9}{1\cdot2}+\frac{9}{2\cdot3}+\frac{9}{3\cdot4}+....+\frac{9}{98\cdot99}+\frac{9}{99\cdot100}\)
cảm ơn nhiều ạ
Chứng minh rằng: \(\frac{1}{2^2}\)+\(\frac{1}{4^2}+\frac{1}{6^2}+...+\frac{1}{100^2}< \frac{1}{2}\)
Bài 1Cho phân số Afrac{n+3}{n-5}
(n∈Z).Tìm n để A nhận giá trị nguyên
Bài 2 Cho phân số Afrac{2n+8}{n+1}
(n∈Z).Tìm các số tự nhiên n để A là số nguyên tố
Bài 3 Chứng minh rằng phân số frac{5n+1}{20n+3}
tối giản với mọi số tự nhiên n
Bài 4 So sánh:
A frac{10^8+2}{10^8-1}
và B frac{10^8}{10^8-3}
Bài 5 Chứng minh:
a, Sfrac{1}{5}+frac{1}{13}+frac{1}{14}+frac{1}{15}+frac{1}{61}+frac{1}{62}+frac{1}{63} frac{1}{2}
b, Pfrac{1}{2}+frac{1}{2^2}+frac{1}{2^3}+........+frac{1}{2^{20}} 1
trả lời n...
Đọc tiếp
Bài 1Cho phân số A=\(\frac{n+3}{n-5}\)
(n∈Z).Tìm n để A nhận giá trị nguyên
Bài 2 Cho phân số A=\(\frac{2n+8}{n+1}\)
(n∈Z).Tìm các số tự nhiên n để A là số nguyên tố
Bài 3 Chứng minh rằng phân số \(\frac{5n+1}{20n+3}\)
tối giản với mọi số tự nhiên n
Bài 4 So sánh:
A= \(\frac{10^8+2}{10^8-1}\)
và B= \(\frac{10^8}{10^8-3}\)
Bài 5 Chứng minh:
a, S=\(\frac{1}{5}+\frac{1}{13}+\frac{1}{14}+\frac{1}{15}+\frac{1}{61}+\frac{1}{62}+\frac{1}{63}< \frac{1}{2}\)
b, P=\(\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+........+\frac{1}{2^{20}}< 1\)
trả lời nhanh hộ mình , mình cần gấp
Cảm ơn
Cho A = \(\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+...+\frac{1}{2^{100}}\). Tính A
Làm giúp hộ mình đi :33 Cần gấp lém đó
Please !!!
Tính
a, A= \(\left(\frac{3}{5}\right)^2.5^2-\left(2\frac{1}{4}\right)^3:\left(\frac{3}{4}\right)^3+\frac{1}{2}\)
b, B= \(\left[\frac{4}{11}.\left(\frac{1}{25}\right)^0+\frac{7}{22}.2\right]^{2010}-\left(\frac{1}{2^2}:\frac{8^2}{4^4}\right)^{2009}\)
Giải hộ bài này giúp mik nhé
Chứng minh rằng:
\(\frac{1}{2}-\frac{1}{4}+\frac{1}{8}-\frac{1}{16}+\frac{1}{32}-\frac{1}{64}<\frac{1}{3}\)
Giúp mình với!!!
Tính tổng S = 1 +\(\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+...+\frac{1}{2^{100}}\)
Các bn ơi, giúp mk, mk đang cần gấp !!!
a) frac{1}{x-1}+frac{-2}{3}(frac{3}{4}-frac{6}{5})frac{5}{2-2x}
b) 3-frac{2}{2x-3}frac{2}{5}+frac{2}{9-6x}-frac{3}{2}
c) frac{x}{2}-frac{1}{x}frac{1}{12}
d) ^{x^2}-frac{7}{6}x+frac{1}{3}0
Mik đang cần gấp! Giúp mik với
Đọc tiếp
a) \(\frac{1}{x-1}\)+\(\frac{-2}{3}\)(\(\frac{3}{4}\)-\(\frac{6}{5}\))=\(\frac{5}{2-2x}\)
b) 3-\(\frac{2}{2x-3}\)=\(\frac{2}{5}\)+\(\frac{2}{9-6x}\)-\(\frac{3}{2}\)
c) \(\frac{x}{2}\)-\(\frac{1}{x}\)=\(\frac{1}{12}\)
d) \(^{x^2}\)-\(\frac{7}{6}x\)+\(\frac{1}{3}\)=0
Mik đang cần gấp! Giúp mik với
Bài 1: Tính giá trị biểu thức:
Afrac{4}{3}+frac{4}{15}+frac{4}{35}+...+frac{4}{9999}
Bài 2: Cho Bfrac{1}{2^2}+frac{1}{3^2}+...+frac{1}{9^2}
Chứng tỏ: frac{2}{5} Bfrac{8}{9}
Bài 3: Tính giá trị biểu thức:
Cfrac{1}{2}-frac{1}{6}-frac{1}{12}-frac{1}{20}-...-frac{1}{9900}
Đọc tiếp
Bài 1: Tính giá trị biểu thức:
\(A=\frac{4}{3}+\frac{4}{15}+\frac{4}{35}+...+\frac{4}{9999}\)
Bài 2: Cho \(B=\frac{1}{2^2}+\frac{1}{3^2}+...+\frac{1}{9^2}\)
Chứng tỏ: \(\frac{2}{5}< B=\frac{8}{9}\)
Bài 3: Tính giá trị biểu thức:
\(C=\frac{1}{2}-\frac{1}{6}-\frac{1}{12}-\frac{1}{20}-...-\frac{1}{9900}\)