Question

Mặt trên của tấm đệm có dạng hình tròn ở Hình 29 gợi nên hình ảnh đường tròn ngoại tiếp hình chữ nhật. Biết hình chữ nhật đó có chiều rộng, chiều dài lần lượt là 3 dm, 5 dm. Tính độ dài đường kính mặt trên của tấm đệm, từ đó tính diện tích mặt trên của tấm đệm.

Answer 1

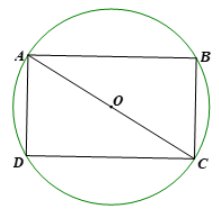
Hình chữ nhật ABCD có chiều dài AB = 5 dm, chiều rộng BC = 3 dm.

Xét tam giác ACB vuông tại B có:

 \(\begin{array}{l}A{B^2} + B{C^2} = A{C^2}(Pytago)\\{5^2} + {3^2} = A{C^2}\\AC = \sqrt {34} dm\end{array}\)

Mà hình chữ nhật ABCD nội tiếp đường tròn nên đường kính tấm đệm là\(AB = \sqrt {34} dm.\)

Diện tích hình tròn là: \(S = \pi .\frac{{{d^2}}}{4} = \pi .\frac{{{{\sqrt {34} }^2}}}{4} = \frac{{17\pi }}{2}d{m^2}.\)