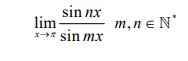Câu 24:
\(\lim\limits_{x\rightarrow2^-}\left[\frac{1}{\left(x-2\right)\left(x-3\right)}-\frac{1}{x-2}\right]=\lim\limits_{x\rightarrow2^-}\left[\frac{1-\left(x-3\right)}{\left(x-2\right)\left(x-3\right)}\right]\)
\(=\lim\limits_{x\rightarrow2^-}\frac{4-x}{\left(x-2\right)\left(x-3\right)}=\lim\limits_{x\rightarrow2^-}\frac{4-x}{\left(2-x\right)\left(3-x\right)}=\frac{2}{0}=+\infty\)
Câu 25:
\(\lim\limits_{x\rightarrow-\infty}\left[\sqrt{x^2+5x}+\sqrt{x^2+8}\right]\)
\(=\lim\limits_{x\rightarrow-\infty}\left[\left|x\right|\left(\sqrt{1+\frac{5}{x}}+\sqrt{1+\frac{8}{x^2}}\right)\right]=+\infty.\left(1+1\right)=+\infty\)
Câu 26:
\(\lim\limits_{x\rightarrow+\infty}\frac{\left(2x+5\right)^3\left(2-x\right)^4}{x^7+1}=\lim\limits_{x\rightarrow+\infty}\frac{x^3\left(2+\frac{5}{x}\right)^3.x^4\left(\frac{2}{x}-1\right)^4}{x^7\left(1+\frac{1}{x^7}\right)}\)
\(=\lim\limits_{x\rightarrow+\infty}\frac{\left(2+\frac{5}{x}\right)^3\left(\frac{2}{x}-1\right)^4}{1+\frac{1}{x^7}}=\frac{2^3.\left(-1\right)^4}{1}=8\)
Câu 27:
\(\lim\limits_{x\rightarrow3}\frac{\sqrt{2x+3}-3+3-\sqrt[3]{7x+6}}{x-3}=\lim\limits_{x\rightarrow3}\frac{\frac{2\left(x-3\right)}{\sqrt{2x+3}+3}-\frac{7\left(x-3\right)}{9+3\sqrt[3]{7x+6}+\sqrt[3]{\left(7x+6\right)^2}}}{x-3}\)
\(=\lim\limits_{x\rightarrow3}\left(\frac{2}{\sqrt{2x+3}+3}-\frac{7}{9+3\sqrt[3]{7x+6}+\sqrt[3]{\left(7x+6\right)^2}}\right)=\frac{2}{3+3}-\frac{7}{9+9+9}=\frac{2}{27}\)
Câu 34:
\(\lim\limits_{x\rightarrow2^+}f\left(x\right)=\lim\limits_{x\rightarrow2^+}\left(x^2+3x-5\right)=5\)
\(\lim\limits_{x\rightarrow2^-}f\left(x\right)=\lim\limits_{x\rightarrow2^-}2=2\)
\(\Rightarrow\lim\limits_{x\rightarrow2^+}f\left(x\right)\ne\lim\limits_{x\rightarrow2^-}f\left(x\right)\)
\(\Rightarrow\) Không tồn tại giới hạn của hàm số khi \(x\rightarrow2\)
35.
\(\lim\limits_{x\rightarrow0}\frac{x\left(1-2cos^2x\right)}{sin2x}=\lim\limits_{x\rightarrow0}\frac{1-2cos^2x}{2.\left(\frac{sin2x}{2x}\right)}=\frac{1-2.1}{2.1}=-\frac{1}{2}\)
36.
Đáp án D đúng
Đề thiếu bạn, giới hạn thì x phải tiến tới đâu chứ?
Câu 21:
\(\lim\limits_{x\rightarrow4}\frac{\sqrt{2x+1}-3}{x^2-5x+4}=\lim\limits_{x\rightarrow4}\frac{\left(\sqrt{2x+1}-3\right)\left(\sqrt{2x+1}+3\right)}{\left(x-4\right)\left(x-1\right)\left(\sqrt{2x+1}+3\right)}\)
\(=\lim\limits_{x\rightarrow4}\frac{2\left(x-4\right)}{\left(x-4\right)\left(x-1\right)\left(\sqrt{2x+1}+3\right)}=\lim\limits_{x\rightarrow4}\frac{2}{\left(x-1\right)\left(\sqrt{2x+1}+3\right)}=\frac{2}{3.\left(3+3\right)}=\frac{1}{9}\)
Câu 22:
Khi \(x\rightarrow3\Rightarrow\left\{{}\begin{matrix}x-1>0\\x+2>0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\left|x-1\right|=x-1\\\left|x+2\right|=x+2\end{matrix}\right.\)
\(\Rightarrow\lim\limits_{x\rightarrow3}\frac{\left|x-1\right|-2}{5-\left|x+3\right|}=\lim\limits_{x\rightarrow3}\frac{x-1-2}{5-\left(x+3\right)}=\lim\limits_{x\rightarrow3}\frac{x-3}{-\left(x-3\right)}=-1\)
Câu 23:
\(\lim\limits_{x\rightarrow2^+}\left[\frac{-40}{\left(x-2\right)\left(x+6\right)}+\frac{5}{x-2}\right]=\lim\limits_{x\rightarrow2^+}\left[\frac{-40+5\left(x+6\right)}{\left(x-2\right)\left(x+6\right)}\right]\)
\(=\lim\limits_{x\rightarrow2^+}\frac{5\left(x-2\right)}{\left(x-2\right)\left(x+6\right)}=\lim\limits_{x\rightarrow2^+}\frac{5}{x+6}=\frac{5}{8}\)
Câu 28:
\(\lim\limits_{x\rightarrow-\infty}\frac{\left(2-3x\right)\left(x+5\right)^2}{-x^3+2}=\lim\limits_{x\rightarrow-\infty}\frac{x\left(\frac{2}{x}-3\right).x^2\left(1+\frac{5}{x}\right)^2}{x^3\left(-1+\frac{2}{x^3}\right)}=\lim\limits_{x\rightarrow-\infty}\frac{\left(\frac{2}{x}-3\right)\left(1+\frac{5}{x}\right)^2}{-1+\frac{2}{x^3}}=\frac{-3.1}{-1}=3\)
Câu 29:
\(\left|\frac{3-2\sqrt{2}}{2}\right|=\left|\frac{\left(3-2\sqrt{2}\right)\left(3+2\sqrt{2}\right)}{2\left(3+2\sqrt{2}\right)}\right|=\frac{1}{2\left(3+2\sqrt{2}\right)}< 1\)
\(\Rightarrow\lim\limits_{x\rightarrow+\infty}\left(\frac{3-2\sqrt{2}}{2}\right)^x=0\)
Câu 30:
\(x\rightarrow-1\Rightarrow x+5>0\Rightarrow\left|x+5\right|=x+5\)
\(\lim\limits_{x\rightarrow-1}\frac{x+5-4}{2-\sqrt{9+5x}}=\lim\limits_{x\rightarrow-1}\frac{\left(x+1\right)\left(2+\sqrt{9+5x}\right)}{\left(2-\sqrt{9+5x}\right)\left(2+\sqrt{9+5x}\right)}\)
\(=\lim\limits_{x\rightarrow-1}\frac{\left(x+1\right)\left(2+\sqrt{9+5x}\right)}{-5\left(x+1\right)}=\lim\limits_{x\rightarrow-1}\frac{2+\sqrt{9+5x}}{-5}=\frac{2+2}{-5}=-\frac{4}{5}\)
Câu 31:
\(\lim\limits_{x\rightarrow-\infty}\frac{\left(3x+5\right)^4\left(2-x\right)^2}{x^4+3}=\lim\limits_{x\rightarrow-\infty}\frac{x^4.\left(3+\frac{5}{x}\right)^4.x^2\left(\frac{2}{x}-1\right)^2}{x^4\left(1+\frac{3}{x^4}\right)}\)
\(=\lim\limits_{x\rightarrow-\infty}\frac{x^2\left(3+\frac{5}{x}\right)^4\left(\frac{2}{x}-1\right)^2}{1+\frac{3}{x^4}}=\frac{+\infty.3^4.\left(-1\right)^2}{1}=+\infty\)
Câu 32:
\(\lim\limits_{x\rightarrow0}\frac{cos6x-cos2x}{x^2}=\lim\limits_{x\rightarrow0}\frac{-2sin4x.sin2x}{x^2}=\lim\limits_{x\rightarrow0}\frac{-4sin2x.cos2x.sin2x}{x^2}\)
\(=\lim\limits_{x\rightarrow0}\left(\frac{sin2x}{2x}\right)^2.\left(-16cos2x\right)=1.\left(-16.1\right)=-16\)
Câu 33:
\(\lim\limits_{x\rightarrow-\infty}x^2.tan^2\frac{1}{2x}=\lim\limits_{x\rightarrow-\infty}\frac{tan^2\frac{1}{2x}}{4\left(\frac{1}{2x}\right)^2}\)
Đặt \(\frac{1}{2x}=t\Rightarrow t\rightarrow0\)
\(\Rightarrow\lim\limits_{t\rightarrow0}\frac{tan^2t}{4t^2}=\lim\limits_{t\rightarrow0}\left(\frac{sint}{t}\right)^2.\frac{1}{4cos^2t}=1.\frac{1}{4.1}=\frac{1}{4}\)
Câu 1:
Mệnh đề I:
\(\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\left(2x+1\right)=2.0+1=1\)
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\left(1-x\right)=1-0=1\)
\(f\left(0\right)=2.0+1=0\)
\(\Rightarrow\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=f\left(0\right)\Rightarrow f\left(x\right)\) liên tục tại \(x=0\)
\(\Rightarrow f\left(x\right)\) liên tục trên R \(\Rightarrow\) đây là mệnh đề đúng
Mệnh đề II:
\(\lim\limits_{x\rightarrow0}f\left(x\right)=\lim\limits_{x\rightarrow0}\frac{2x+1}{x}=\frac{2.0+1}{0}=+\infty\)
\(\Rightarrow f\left(x\right)\) ko liên tục tại \(x=0\Rightarrow\) đây là mệnh đề sai
Câu 2:
\(\lim\limits_{x\rightarrow0}f\left(x\right)=\lim\limits_{x\rightarrow0}\frac{\sqrt{x+2}-\sqrt{2-x}}{x}=\lim\limits_{x\rightarrow0}\frac{\left(\sqrt{x+2}-\sqrt{2-x}\right)\left(\sqrt{x+2}+\sqrt{2-x}\right)}{x\left(\sqrt{x+2}+\sqrt{2-x}\right)}\)
\(=\lim\limits_{x\rightarrow0}\frac{2x}{x\left(\sqrt{x+2}+\sqrt{2-x}\right)}=\lim\limits_{x\rightarrow0}\frac{2}{\sqrt{x+2}+\sqrt{2-x}}=\frac{2}{2\sqrt{2}}=\frac{1}{\sqrt{2}}\)
\(\Rightarrow\) Để \(f\left(x\right)\) liên tục tại \(x=0\)
\(\Leftrightarrow f\left(0\right)=\lim\limits_{x\rightarrow0}f\left(x\right)=\frac{1}{\sqrt{2}}\)
Câu 3:
Xét tại \(x=0\)
\(\lim\limits_{x\rightarrow0}f\left(x\right)=\lim\limits_{x\rightarrow0}\frac{x^2}{x}=\lim\limits_{x\rightarrow0}x=0\)
\(\Rightarrow\lim\limits_{x\rightarrow0}f\left(x\right)=f\left(0\right)\Rightarrow f\left(x\right)\) liên tục tại \(x=0\)
Xét tại \(x=1\)
\(\lim\limits_{x\rightarrow1^+}f\left(x\right)=\lim\limits_{x\rightarrow1^+}\sqrt{x}=\sqrt{1}=1\)
\(\lim\limits_{x\rightarrow1^-}f\left(x\right)=\lim\limits_{x\rightarrow1^-}\frac{x^2}{x}=\lim\limits_{x\rightarrow1^-}x=1\)
\(f\left(1\right)=\sqrt{1}=1\)
\(\Rightarrow\lim\limits_{x\rightarrow1^-}f\left(x\right)=\lim\limits_{x\rightarrow1^+}f\left(x\right)=f\left(1\right)\Rightarrow f\left(x\right)\) liên tục tại \(x=1\)
\(\Rightarrow f\left(x\right)\) liên tục trên R
Câu 4:
\(f\left(x\right)\) ko liên tục tại \(x=1\) (để ý tại x=1 đồ thị của hàm số rời hẳn nhau ra chứ ko nối liền với nhau)
Câu 5:
\(x^2+5x+6=0\Rightarrow\left[{}\begin{matrix}x=-2\\x=-3\end{matrix}\right.\)
\(\Rightarrow f\left(x\right)\) ko xác định tại \(x=-2;x=-3\)
\(\Rightarrow f\left(x\right)\) ko liên tục tại \(x=-2;x=-3\)
\(\Rightarrow f\left(x\right)\) liên tục trên các khoảng: \(\left(-\infty;-3\right)\cup\left(-3;-2\right)\cup\left(-2;+\infty\right)\)
\(\Rightarrow\) Chỉ có đáp án D đúng (là tập con của \(\left(-2;+\infty\right)\))