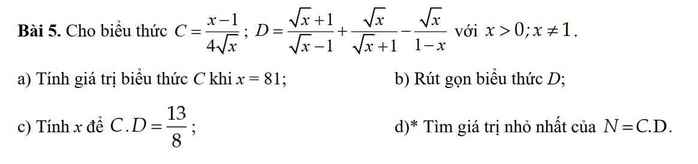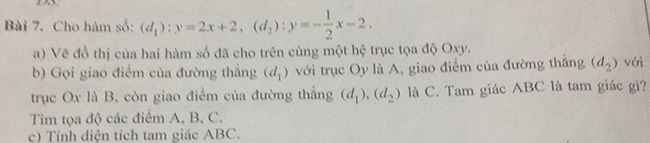\(a,C=\dfrac{81-1}{4\cdot9}=\dfrac{80}{36}=\dfrac{20}{9}\\ b,D=\dfrac{x+2\sqrt{x}+1+x-\sqrt{x}+\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ D=\dfrac{2x+2\sqrt{x}+1}{x-1}\\ c,CD=\dfrac{x-1}{4\sqrt{x}}\cdot\dfrac{2x+2\sqrt{x}+1}{x-1}=\dfrac{2x+2\sqrt{x}+1}{4\sqrt{x}}=\dfrac{13}{8}\\ \Leftrightarrow52\sqrt{x}=16x+16\sqrt{x}+8\\ \Leftrightarrow16x-36\sqrt{x}+8=0\\ \Leftrightarrow4x-9\sqrt{x}+2=0\\ \Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=2\\\sqrt{x}=\dfrac{1}{4}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\left(tm\right)\\x=\dfrac{1}{16}\left(tm\right)\end{matrix}\right.\)
\(d,N=CD=\dfrac{2x+2\sqrt{x}+1}{4\sqrt{x}}=\dfrac{\sqrt{x}}{2}+\dfrac{1}{2}+\dfrac{1}{4\sqrt{x}}\\ \Leftrightarrow N\ge2\sqrt{\dfrac{\sqrt{x}}{2}\cdot\dfrac{1}{4\sqrt{x}}}+\dfrac{1}{2}=2\sqrt{\dfrac{1}{8}}+\dfrac{1}{2}=\dfrac{\sqrt{2}+1}{2}\)
Dấu \("="\Leftrightarrow4x=2\Leftrightarrow x=\dfrac{1}{2}\left(tm\right)\)
Vậy \(N_{min}=\dfrac{\sqrt{2}+1}{2}\)