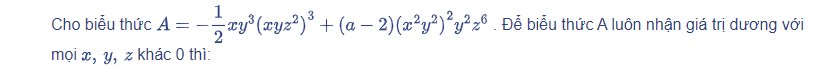\(A=-\dfrac{1}{2}xy^3\cdot\left(xyz^2\right)^3+\left(a-2\right)\cdot\left(x^2y^2\right)^2\cdot y^2z^6\)
\(=-\dfrac{1}{2}xy^3\cdot x^3y^3z^6+\left(a-2\right)\cdot x^4y^4\cdot y^2z^6\)
\(=-\dfrac{1}{2}x^4y^6z^6+\left(a-2\right)\cdot x^4y^6z^6\)
\(=x^4y^6z^6\left(-\dfrac{1}{2}+a-2\right)=\left(a-\dfrac{5}{2}\right)\cdot x^4y^6z^6\)
Để A>0 với mọi x,y,z khác 0 thì \(a-\dfrac{5}{2}>0\)
=>\(a>\dfrac{5}{2}\)
Đúng 2
Bình luận (0)