\(B=\left(3a-\dfrac{1}{2}\right)xy^4z^2\cdot\left(xy^2\right)^3+\left(a-1\right)\cdot y^2z^2\cdot\left(xy^2\right)^4\)
\(=\left(3a-\dfrac{1}{2}\right)\cdot xy^4z^2\cdot x^3y^6+\left(a-1\right)\cdot y^2z^2\cdot x^4y^8\)
\(=\left(3a-\dfrac{1}{2}\right)\cdot x^4y^{10}z^2+\left(a-1\right)\cdot x^4y^{10}z^2\)
\(=\left(3a-\dfrac{1}{2}+a-1\right)\cdot x^4y^{10}z^2\)
\(=\left(4a-\dfrac{3}{2}\right)\cdot x^4y^{10}z^2\)
Để B<0 thì \(4a-\dfrac{3}{2}< 0\)
=>\(4a< \dfrac{3}{2}\)
=>\(a< \dfrac{3}{2}:4=\dfrac{3}{8}\)
Đúng 3
Bình luận (0)

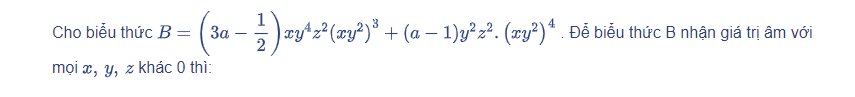 k cần giải chi tiết đâu ạ
k cần giải chi tiết đâu ạ

