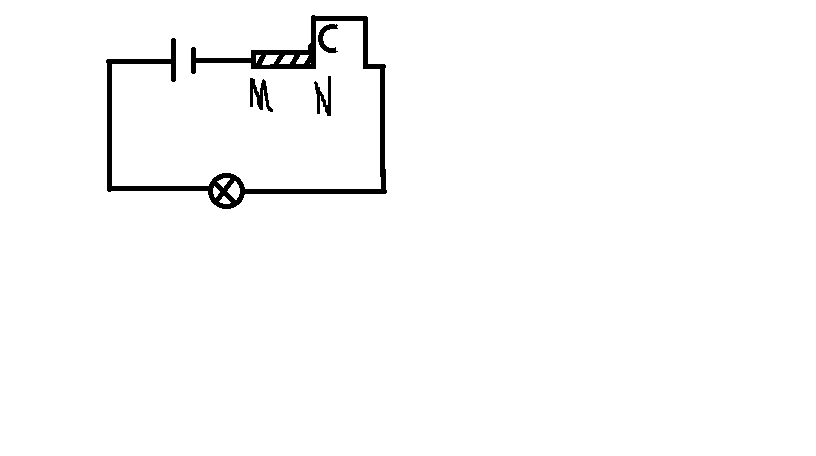
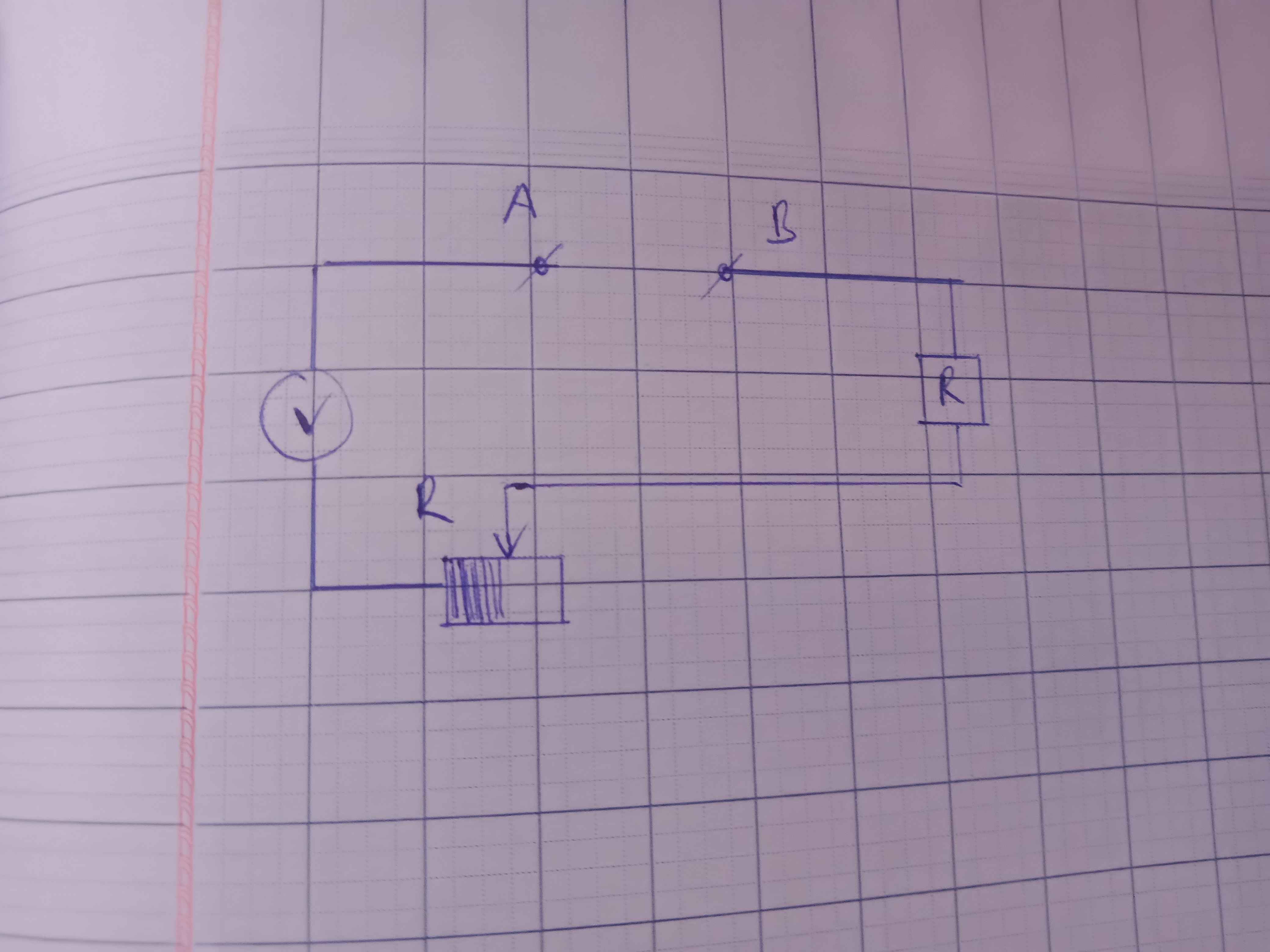
Giả sử hiệu điện thế ban đầu là \(U\), hai đầu biến trở lần lượt từ trái sang phải là \(M,N.\)
Cấu trúc mạch: \(\left(R\left|\right|R_{MC}\right)\text{ nt }R_{CN}\).
Đặt: \(R_{MC}=x\left(0\le x\le R\right)\).
Với hiệu điện thế \(U\): \(R_{MC}=R_{CN}=\dfrac{1}{2}R\left(x=\dfrac{1}{2}\right)\).
Cường độ dòng điện qua mạch chính:
\(I=\dfrac{U}{\dfrac{RR_{MC}}{R+R_{MC}}+R_{CN}}=\dfrac{U}{\dfrac{R\cdot\dfrac{1}{2}R}{R+\dfrac{1}{2}R}+\dfrac{1}{2}R}=\dfrac{6U}{5R}\)
Hiệu điện thế hai đầu điện trở R:
\(U_R=I\cdot\dfrac{RR_{MC}}{R+R_{CN}}=\dfrac{6U}{5R}\cdot\dfrac{R\cdot\dfrac{1}{2}R}{R+\dfrac{1}{2}R}=\dfrac{2}{5}U\)
Với hiệu điện thế \(2U\): \(R_{CN}=R-x\).
Điện trở tương đương của đoạn mạch:
\(R_{tđ}=\dfrac{RR_{MC}}{R+R_{MC}}+R_{CN}=\dfrac{Rx}{R+x}+R-x=\dfrac{R^2+Rx-x^2}{R+x}\)
Cường độ dòng điện qua mạch chính:
\(I=\dfrac{2U}{R_{tđ}}=\dfrac{2U}{\dfrac{R^2+Rx-x^2}{R+x}}=\dfrac{2U\left(R+x\right)}{R^2+Rx-x^2}\)
Hiệu điện thế hai đầu điện trở R lúc này:
\(U_R'=I\cdot\dfrac{RR_{MC}}{R+R_{MC}}=\dfrac{2U\left(R+x\right)}{R^2+Rx-x^2}\cdot\dfrac{Rx}{R+x}=\dfrac{2URx}{R^2+Rx-x^2}\)
Theo đề: \(U_R=U_R'\Leftrightarrow\dfrac{2}{5}U=\dfrac{2URx}{R^2+Rx-x^2}\)
\(\Leftrightarrow R^2+Rx-x^2=5Rx\)
\(\Leftrightarrow R^2-4Rx-x^2=0\)
Giải phương trình trên với ẩn x:
\(\Delta'=\left(-2R\right)^2-\left(-1\right)R^2=5R^2\Leftrightarrow\sqrt{\Delta}=R\sqrt{5}\)
\(\Rightarrow\left[{}\begin{matrix}x_1=\dfrac{-\left(-2R\right)+R\sqrt{5}}{-1}=-2-R\sqrt{5}\\x_2=\dfrac{-\left(-2R\right)-R\sqrt{5}}{-1}=-2+R\sqrt{5}\end{matrix}\right.\)
Với nghiệm x1: \(0\le x_1\le R\)
\(\Leftrightarrow0\le-2-R\sqrt{5}\le R\Rightarrow R\in\varnothing\).
Do đó, loại nghiệm x1.
Với nghiệm x2: \(0\le x_2\le R\)
\(\Leftrightarrow0\le-2+R\sqrt{5}\le R\Rightarrow\dfrac{2\sqrt{5}}{5}\le R\le\dfrac{\sqrt{5}+1}{2}\).
Do đó, nhận nghiệm x2.
Ta có: \(\Delta x=\left|x-x_2\right|=\left|\dfrac{1}{2}-\left(-2+R\sqrt{5}\right)\right|=\left|\dfrac{5}{2}+R\sqrt{5}\right|=\dfrac{5}{2}+R\sqrt{5}\)
Vậy: Phải dịch chuyển con chạy C về phía M, tức theo hướng của điểm A một đoạn \(\Delta x=\dfrac{5}{2}+R\sqrt{5}\).