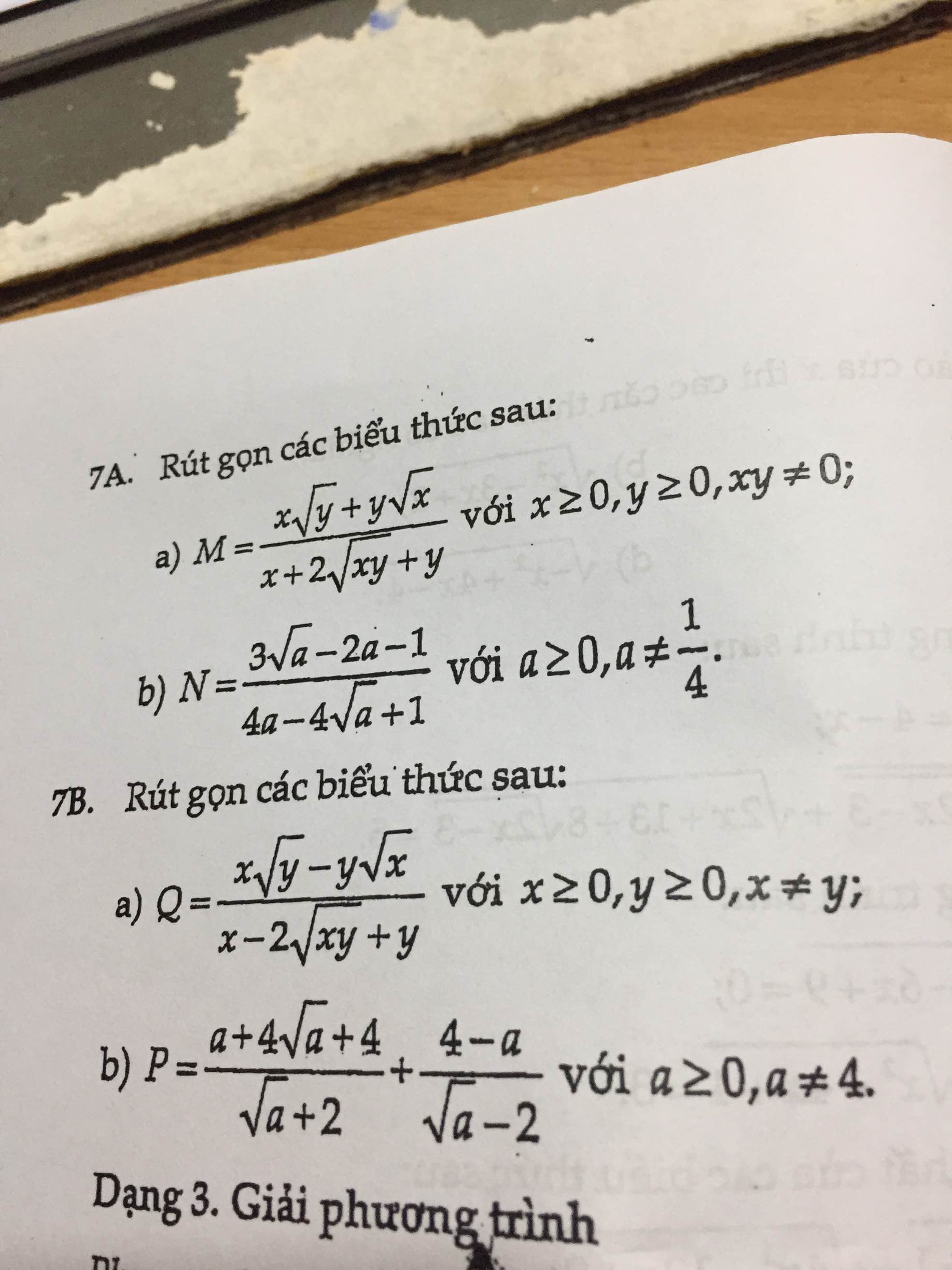7A
M=\(\dfrac{\sqrt{xy}\left(\sqrt{x}+\sqrt{y}\right)}{\left(\sqrt{x}+\sqrt{y}\right)^2}\) M= \(\dfrac{\sqrt{xy}}{\sqrt{x}+\sqrt{y}}\)
N = \(\dfrac{3\sqrt{a}-6a+4a-1}{\left(2\sqrt{a}-1\right)^2}\) N= \(\dfrac{-3\sqrt{a}\left(2\sqrt{a}-1\right)+\left(2\sqrt{a}-1\right).\left(2\sqrt{a}+1\right)}{\left(2\sqrt{a}-1\right)^2}\)
N= \(\dfrac{\left(2\sqrt{a}-1\right).\left(1-\sqrt{a}\right)}{\left(2\sqrt{a}-1\right)^2}\) N= \(\dfrac{1-\sqrt{a}}{2\sqrt{a}-1}\)
7B
Q= \(\dfrac{\sqrt{xy}\left(\sqrt{x}-\sqrt{y}\right)}{\left(\sqrt{x}-\sqrt{y}\right)^2}\) Q= \(\dfrac{\sqrt{xy}}{\sqrt{x}-\sqrt{y}}\)
P= \(\dfrac{\left(\sqrt{a}+2\right)^2}{\sqrt{a}+2}-\dfrac{\left(\sqrt{a}-2\right).\left(\sqrt{a}+2\right)}{\sqrt{a}-2}\)
P= \(\sqrt{a}+2-\sqrt{a}-2\) ; P = 0