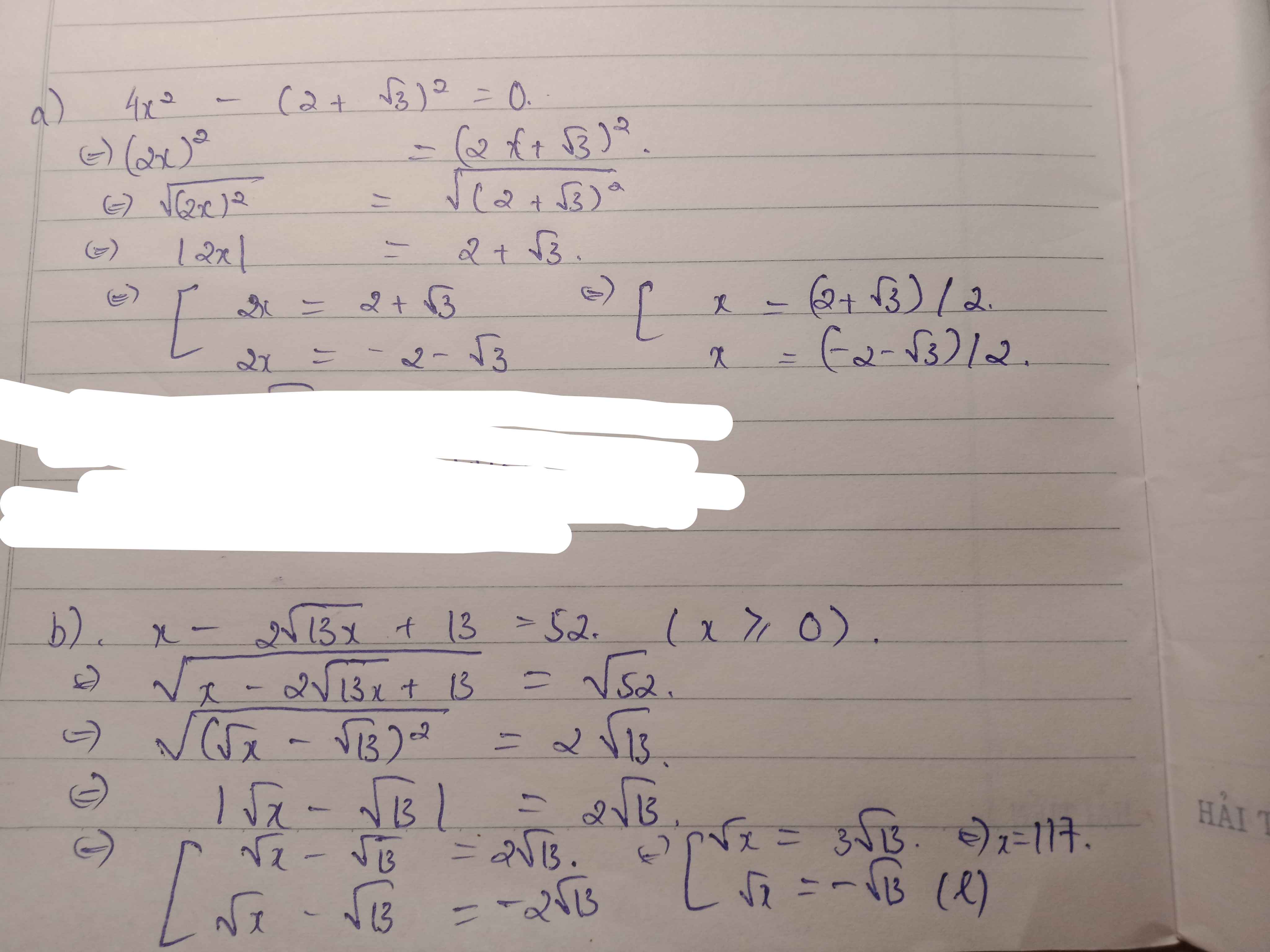\(a,\Leftrightarrow\left(2x-2-\sqrt{3}\right)\left(2x+2+\sqrt{3}\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}2x=2+\sqrt{3}\\2x=-2-\sqrt{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2+\sqrt{3}}{2}\\x=\dfrac{-2-\sqrt{3}}{2}\end{matrix}\right.\\ b,ĐK:x\ge0\\ PT\Leftrightarrow\left(\sqrt{x}-\sqrt{13}\right)^2-\left(2\sqrt{13}\right)^2=0\\ \Leftrightarrow\left(\sqrt{x}-3\sqrt{13}\right)\left(\sqrt{x}+\sqrt{13}\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=3\sqrt{13}\\\sqrt{x}=-\sqrt{13}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=117\left(tm\right)\\x\in\varnothing\left(\sqrt{x}\ge0\right)\end{matrix}\right.\\ \Leftrightarrow x=117\)
Bài 3: Liên hệ giữa phép nhân và phép khai phương
Đúng 1
Bình luận (0)
Các câu hỏi tương tự

giúp mik vs

GIẢI giùm mik Câu C vs
Giúp em vs 1,2 giải denta nha🙁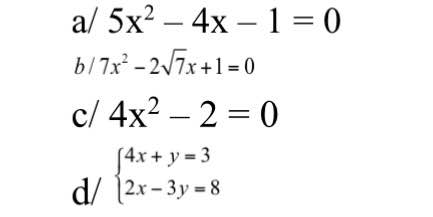
Làm giúp mik câu c, d (bài 3, màu trắng) và bài tập giải phương trình (màu trắng). Cảm ơn ạ

giup vs mn ơi mik đag gấp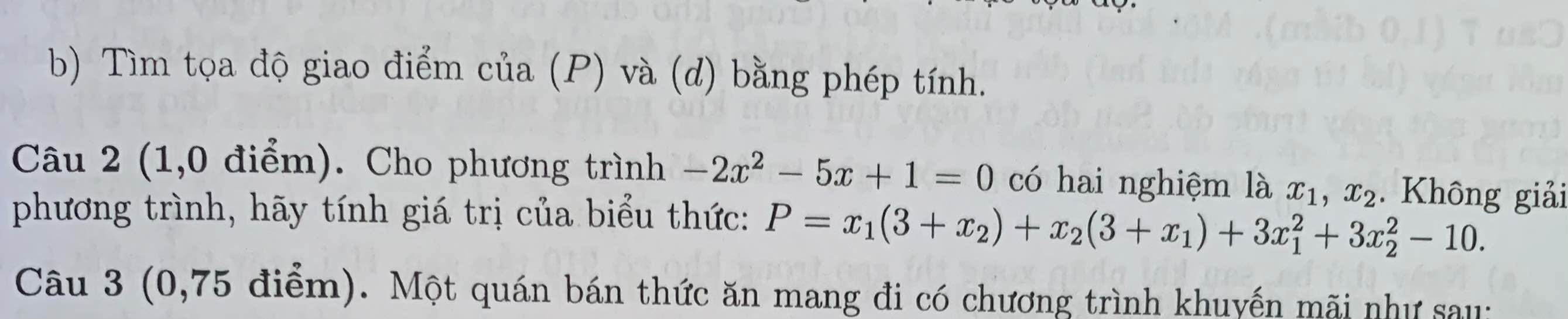
Giúp mình vs ạ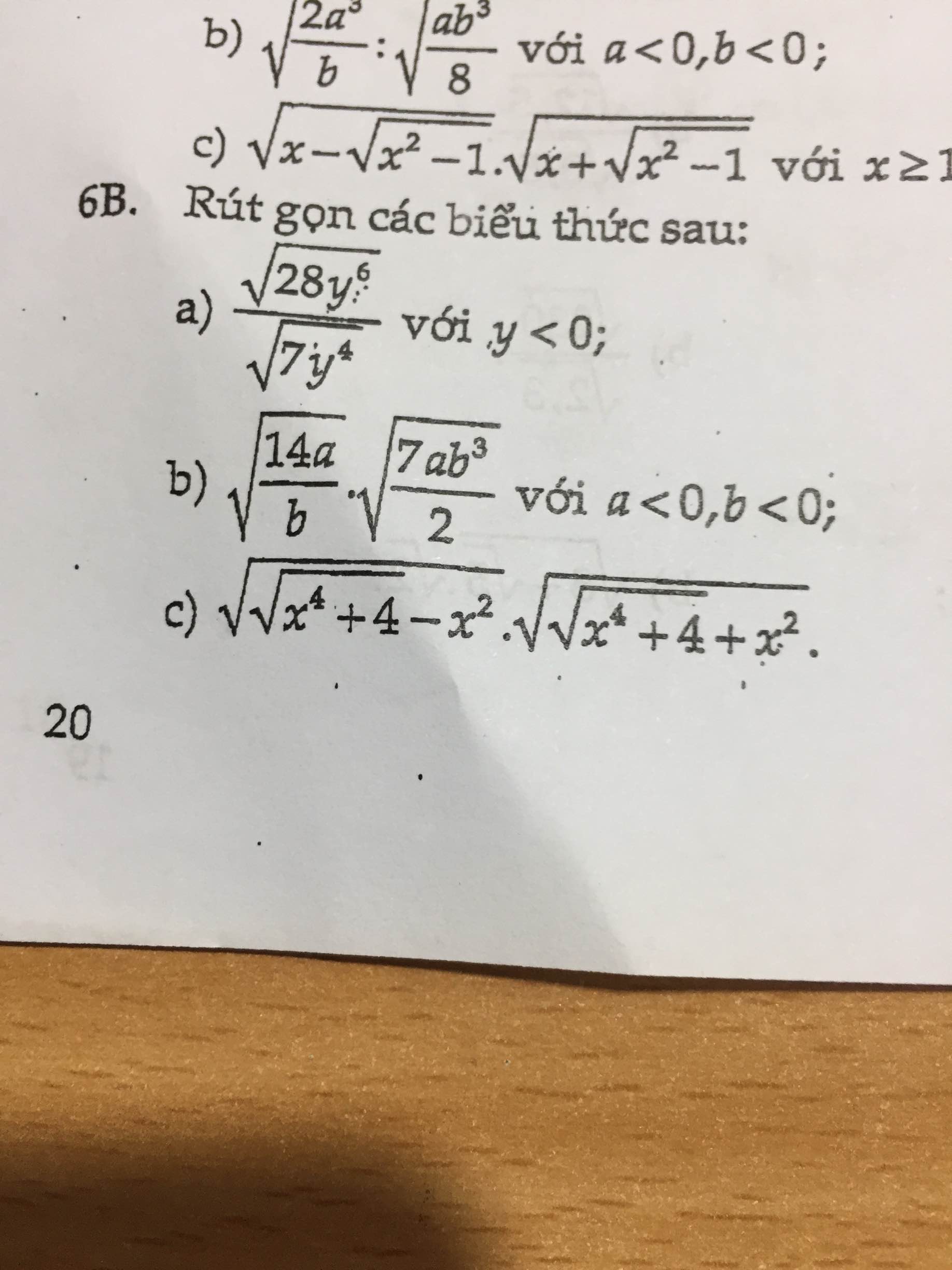
Làm giúp mik câu c, d (bài 3, màu trắng)

Tìm GTNN của B= \(\sqrt{x}+\frac{36}{\sqrt{x}+2}\) với x khác 9 và x =>0 giúp mik vs
giải hộ mik bài 26 trang 9 sbt toán 9 với