11.
Gọi chiều dài và chiều rộng của hình chữ nhật ban đầu là x và y (x>y;x>2;y>1)
Diện tích ban đầu: \(xy\)
Diện tích sau khi tăng mỗi cạnh thêm 1cm: \(\left(x+1\right)\left(y+1\right)\)
Diện tích sau khi giảm chiều dài đi 2 và rộng đi 1: \(\left(x-2\right)\left(y-1\right)\)
Theo bài ra ta có hệ:
\(\left\{{}\begin{matrix}\left(x+1\right)\left(y+1\right)=xy+13\\\left(x-2\right)\left(y-1\right)=xy-15\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+y=12\\x+2y=17\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=7\\y=5\end{matrix}\right.\)
12.
Gọi chiều dài của mảnh đất ban đầu là 0<x<40 thì chiều rộng là \(40-x\)
Diện tích ban đầu: \(x\left(40-x\right)\)
Diện tích sau khi tăng chiều dài thêm 3 và chiều rộng thêm 5 là: \(\left(x+3\right)\left(45-x\right)\)
Theo bài ra ta có pt:
\(\left(x+3\right)\left(45-x\right)=x\left(40-x\right)+195\)
\(\Leftrightarrow2x=60\Rightarrow x=30\)
Vậy mảnh đất dài 30 rộng 10
13.
Gọi số dãy ghế là x và số ghế trong mỗi dãy là y
\(\Rightarrow xy=40\)
Sau khi kê thêm 1 dãy và mỗi dãy thêm 1 chỗ thì số ghế là: \(\left(x+1\right)\left(y+1\right)\)
Ta có hệ:
\(\left\{{}\begin{matrix}xy=40\\\left(x+1\right)\left(y+1\right)=55\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}xy=40\\x+y=14\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=10\\y=4\end{matrix}\right.\) hoặc \(\left\{{}\begin{matrix}x=4\\y=10\end{matrix}\right.\)
Vậy ban đầu trong phòng họp có 4 dãy hoặc 10 dãy ghế








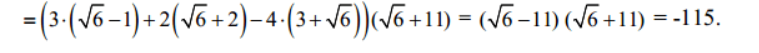

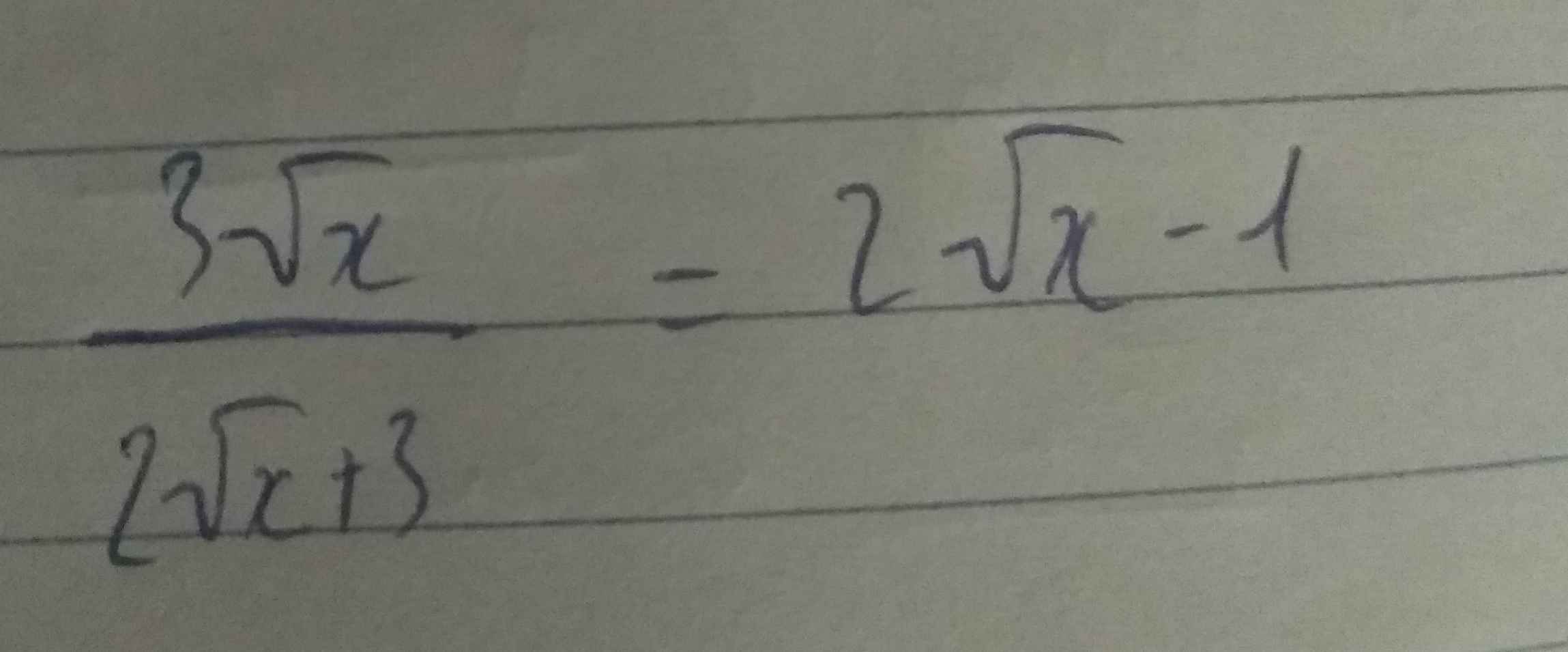







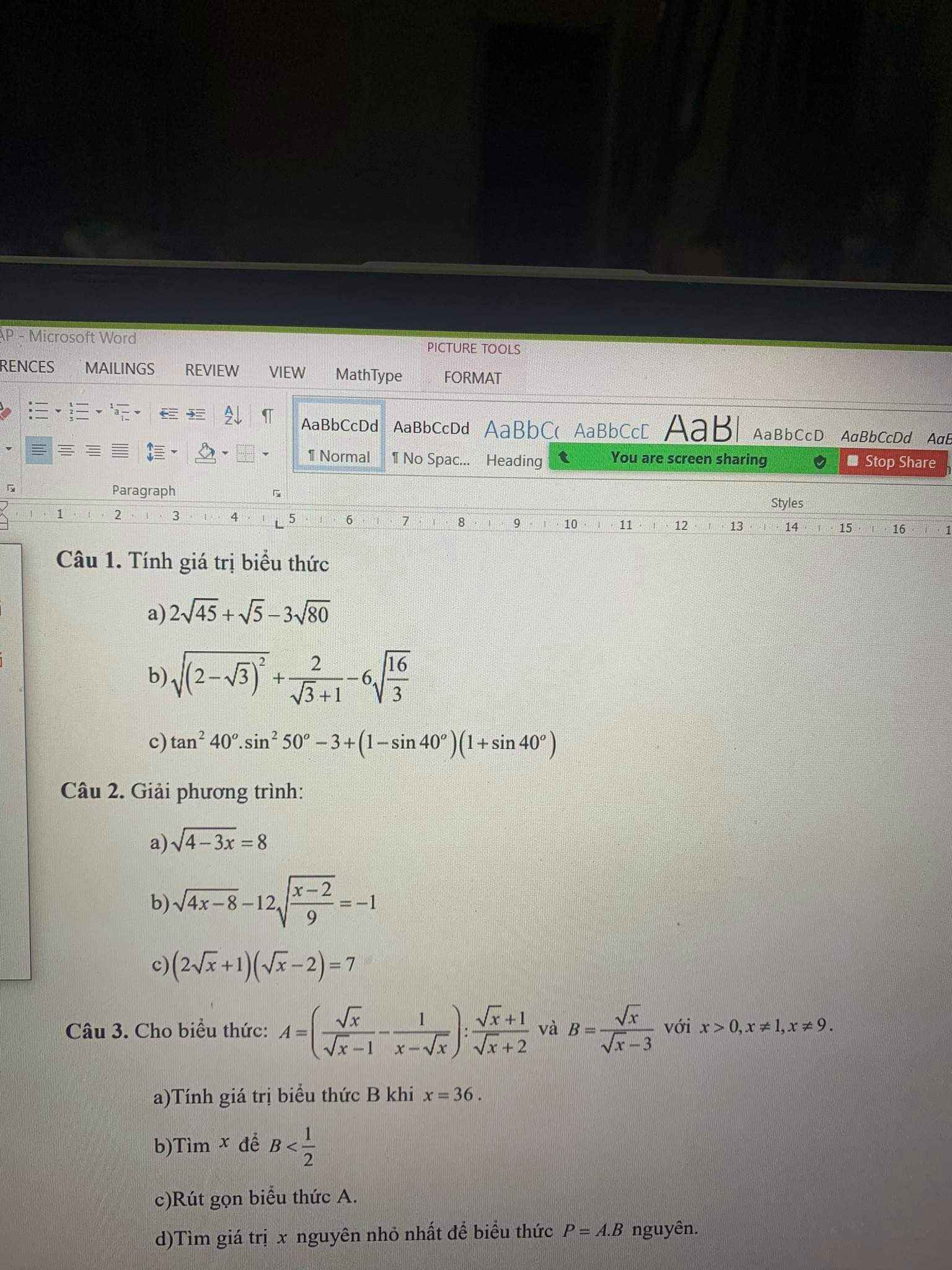

 Mn giúp mình bài 3 với ạ. Mình đang cần gấp lắm. Mình cảm ơn nhiều !
Mn giúp mình bài 3 với ạ. Mình đang cần gấp lắm. Mình cảm ơn nhiều !