Hình 20 minh họa hình ảnh một tòa nhà trong không gian với hệ tọa độ Oxyz (đơn vị trên mỗi trục tọa độ là mét). Biết A(50; 0; 0), D(0; 20; 0), B(4k; 3k; 2k) với k > 0 và mặt phẳng (CBEF) có phương trình là z = 3.
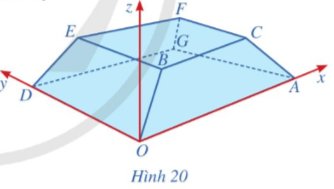
a) Tìm tọa độ của điểm B.
b) Lập phương trình mặt phẳng (AOBC).
c) Lập phương trình mặt phẳng (DOBE).
d) Chỉ ra một vectơ pháp tuyến của mỗi mặt phẳng (AOBC) và (DOBE).
a) Ta có \(B \in (CBEF):2k = 3 \Leftrightarrow k = \frac{3}{2}\).
Vậy \(B(6;\frac{9}{2};3)\).
b) \(\overrightarrow {OA} = (50;0;0);\overrightarrow {OB} = (6;\frac{9}{2};3)\).
Vecto pháp tuyến của mặt phẳng (AOBC) là: \(\overrightarrow {{n_1}} = \left[ {\overrightarrow {OA} ;\overrightarrow {OB} } \right] = (0; - 150;225) = 75(0; - 2;3)\).
Phương trình mặt phẳng (AOB) là: -2y + 3z = 0.
Vậy phương trình mặt phẳng (AOBC) là -2y + 3z = 0.
c) \(\overrightarrow {OD} = (0;20;0)\).
Vecto pháp tuyến của mặt phẳng (AOBC) là: \(\overrightarrow {{n_2}} = \left[ {\overrightarrow {OD} ;\overrightarrow {OB} } \right] = (60;0; - 120) = 60(1;0; - 2)\).
Phương trình mặt phẳng (DOB) là: x - 2z = 0.
Vậy phương trình mặt phẳng (DOBE) là x - 2z = 0.
d) Vecto pháp tuyến của mặt phẳng (AOBC) và (DOBE) lần lượt là \(\overrightarrow {{n_1}} = (0; - 2;3)\) và \(\overrightarrow {{n_2}} = (1;0; - 2)\).


