Ôn tập chương Đường thẳng vuông góc. Đường thẳng song song
Các câu hỏi tương tự
Hình 14 :
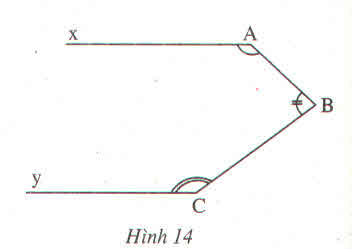
Cho biết \(\widehat{A}+\widehat{B}+\widehat{C}=360^0\)
Chứng minh rằng Ax // Cy ?
Cho widehat{xoy}70^o. Trên tia Ox lấy điểm A vẽ widehat{xAt}70^o
a) Chứng minh rằng Oy//At
b) Qua A kẻ AHperp Oy chứng minh rằng AHperp AT
c) Tính widehat{OAH}
d) Kẻ đường thẳng d là đường trung trực của AH, chứng minh dcap Ox tại B, dcap AH tại I.Chứng minhwidehat{OBI}widehat{OAT}
Đọc tiếp
Cho \(\widehat{xoy}=70^o\). Trên tia Ox lấy điểm A vẽ \(\widehat{xAt}=70^o\)
a) Chứng minh rằng Oy//At
b) Qua A kẻ \(AH\perp Oy\) chứng minh rằng \(AH\perp AT\)
c) Tính \(\widehat{OAH}\)
d) Kẻ đường thẳng d là đường trung trực của AH, chứng minh \(d\cap Ox\) tại B, \(d\cap AH\) tại I.Chứng minh\(\widehat{OBI}=\widehat{OAT}\)
Hình 41 cho biết d // d' // d" và hai góc \(60^0,100^0\). Tính các góc \(\widehat{E}_1,\widehat{G_2},\widehat{G}_3,\widehat{D}_4,\widehat{A}_5,\widehat{B}_6\) ?

Cho hình vẽ. Chứng minh rằng \(\widehat{xAc}\)= \(\widehat{B}+\widehat{C}\)
1)Cho widehat{AOB50^0}gọi OC là tia phân giác của widehat{AOB}.Vẽ tia OE là tia đối của tia OA.Vẽ tia OD vuông góc với OC(tia nằm trong widehat{BOE}).Hãy chứng tỏ rằng tiaOD là tia phân giác củawidehat{BOE}?
2)Cho widehat{AOB130^0} trongwidehat{AOB} vẽ các tia OC ,OD sao cho OC perp OA, ODperp OB.Tính widehat{COD}?
Đọc tiếp
1)Cho \(\widehat{AOB=50^0}\)gọi OC là tia phân giác của \(\widehat{AOB}\).Vẽ tia OE là tia đối của tia OA.Vẽ tia OD vuông góc với OC(tia nằm trong \(\widehat{BOE}\)).Hãy chứng tỏ rằng tiaOD là tia phân giác của\(\widehat{BOE}\)?
2)Cho \(\widehat{AOB=130^0}\) trong\(\widehat{AOB}\) vẽ các tia OC ,OD sao cho OC \(\perp OA\), \(OD\perp OB\).Tính \(\widehat{COD}\)?
Cho tam giác ABC. Dựng ra phía ngoài tam giác ABC tam giác APB đều và tam giác ACE cân tại E sao cho widehat{CEA}120^0. Dựng ram giác BCD cân tại D sao cho widehat{BDC}120^0 và A, D cùng thuộc nửa mặt phẳng có bờ là đường thẳng BC. Dựng tam giác DÈ cân tại D sao cho widehat{EDF}120^0 và F,B cùng thuộc nửa mặt phẳng có bờ là đường thẳng DE. Chứng minh rằng PF CE.
Giúp với ạ @Akai Haruma, @Nguyễn Việt Lâm
Đọc tiếp
Cho tam giác ABC. Dựng ra phía ngoài tam giác ABC tam giác APB đều và tam giác ACE cân tại E sao cho \(\widehat{CEA}=120^0\). Dựng ram giác BCD cân tại D sao cho \(\widehat{BDC}=120^0\) và A, D cùng thuộc nửa mặt phẳng có bờ là đường thẳng BC. Dựng tam giác DÈ cân tại D sao cho \(\widehat{EDF}=120^0\) và F,B cùng thuộc nửa mặt phẳng có bờ là đường thẳng DE. Chứng minh rằng PF = CE.
Giúp với ạ @Akai Haruma, @Nguyễn Việt Lâm
Bài 1: Cho hình vẽ, biết nperp AB tại B, widehat{F_1}120^o.a) Chứng tỏ m//n.b) Tính widehat{E_1}.c) Chứng tỏ mperp AB. Vì sao? E 1 ? F A m n B 120 độ 1
Đọc tiếp
Bài 1: Cho hình vẽ, biết \(n\perp AB\) tại B, \(\widehat{F_1}\)=\(120^o\).
a) Chứng tỏ m//n.
b) Tính \(\widehat{E_1}\).
c) Chứng tỏ \(m\perp AB\). Vì sao?
Bài 4:Cho hình vẽ, biết aperpMP tại M, bperp NQ tại Q, widehat{N_1}65^O.a) Chứng tỏ a//b.b) Tính widehat{M_1}? M P Q a b 1 1 65 độ N
Đọc tiếp
Bài 4:Cho hình vẽ, biết a\(\perp\)MP tại M, \(b\perp NQ\) tại Q, \(\widehat{N_1}\)=\(65^O\).
a) Chứng tỏ a//b.
b) Tính \(\widehat{M_1}\)=?
Bài 1 :Cho DeltaABC . Trên cạnh AB lấy M , trên nửa mặt phẳng bờ AB chứa C , vẽ tia Mx sao cho widehat{AMB}
a) Chứng minh rằng : Mx // BC và Mx cắt AC
b) Gọi D là giao điểm của Mx với AC . Lấy N nằm giữa C và D . Trên nửa mặt phẳng bờ AC khi chứa điểm B . Vẽ tia Ny sao cho widehat{CNY}widehat{C} . Chứng minh rằng : Mx // Ny
Đọc tiếp
Bài 1 :Cho \(\Delta\)ABC . Trên cạnh AB lấy M , trên nửa mặt phẳng bờ AB chứa C , vẽ tia Mx sao cho \(\widehat{AMB}\)
a) Chứng minh rằng : Mx // BC và Mx cắt AC
b) Gọi D là giao điểm của Mx với AC . Lấy N nằm giữa C và D . Trên nửa mặt phẳng bờ AC khi chứa điểm B . Vẽ tia Ny sao cho \(\widehat{CNY}\)=\(\widehat{C}\) . Chứng minh rằng : Mx // Ny











