a) \(\sqrt{12}-4\sqrt{75}-3\sqrt{27}+5\sqrt{48}\)
= \(2\sqrt{3}-20\sqrt{3}-9\sqrt{3}+20\sqrt{3}\)
= \(2\sqrt{3}-9\sqrt{3}\)
= \(-7\sqrt{3}\)
b)\(\sqrt{\left(1-2\sqrt{7}\right)^2}+\sqrt{8+2\sqrt{7}}\)
= \(\sqrt{\left(1-2\sqrt{7}\right)^2}+\sqrt{1+2\sqrt{7}+7}\)
= \(2\sqrt{7}-1+\sqrt{\left(1+\sqrt{7}\right)^2}\)
= \(2\sqrt{7}-1+1+\sqrt{7}\)
= \(3\sqrt{7}\)
c) \(\dfrac{1}{1-\sqrt{3}}-\dfrac{1}{1+\sqrt{3}}\)
= \(\dfrac{1+\sqrt{3}}{\left(1-\sqrt{3}\right)\left(1+\sqrt{3}\right)}-\dfrac{1-\sqrt{3}}{\left(1+\sqrt{3}\right)\left(1-\sqrt{3}\right)}\)
= \(\dfrac{1+\sqrt{3}-1+\sqrt{3}}{1-3}\)
= \(\dfrac{2\sqrt{3}}{-2}=-\sqrt{3}\)





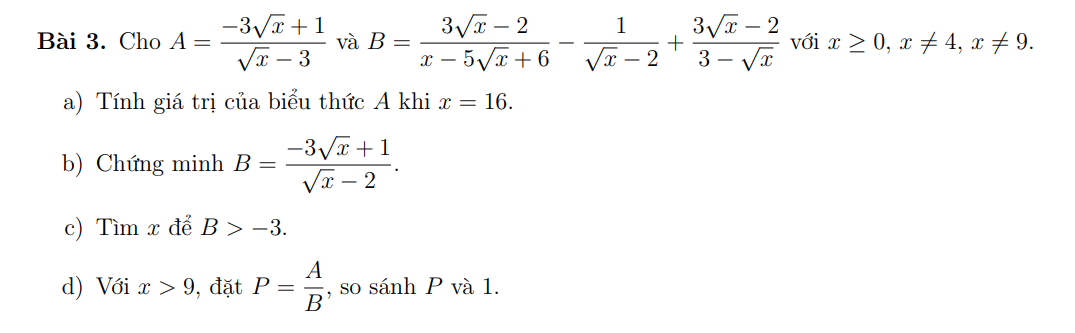 help me !!!
help me !!!








