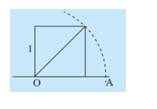
\(\begin{array}{l}5 \in \mathbb{Z};\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - 2 \in \mathbb{Q};\,\,\,\,\,\,\,\,\,\,\,\,\,\sqrt 2 \notin \mathbb{Q};\\\frac{3}{5} \in \mathbb{Q};\,\,\,\,\,\,\,\,\,\,\,\,2,31\left( {45} \right) \notin I\,\,\,\,\,\,7,62\left( {38} \right) \in \mathbb{R};\,\,\,\,0 \notin I\end{array}\)
\(5\in Z\) (do 5 có thể viết ở dạng không ở thành phần phân số);
\(-2\in Q\) (do \(-2\) có thể viết ở dạng phân số có tử số và mẫu số là các số nguyên: \(-2=\dfrac{-2}{1}\));
\(\sqrt{2}\notin Q\) (do \(\sqrt{2}\) không thể viết được ở dạng phân số);
\(\dfrac{3}{5}\in Q\) (dạng phân số có tử số và mẫu số là số nguyên);
\(2,31\left(45\right)\notin I\) (do là số thập phân vô hạn tuần hoàn, có thể biểu diễn ở dạng số hữu tỉ \(\dfrac{1273}{550}\))
\(7,62\left(38\right)\in R\) (do là số thập phân vô hạn tuần hoàn, hay là số hữu tỉ, cũng là số thực)
\(0\notin I\) (do 0 viết được ở dạng phân số, hay là số hữu tỉ)