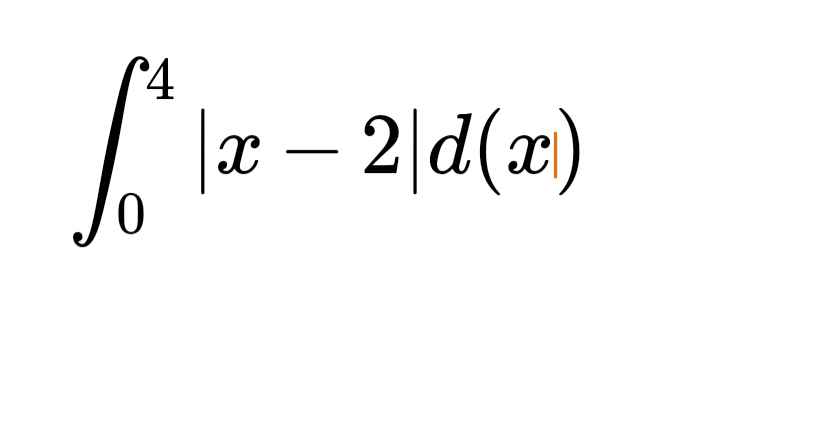Bài 2: Tích phân
Các câu hỏi tương tự
Sử dụng phương pháp tính tích phân từng phần, hãy tính :
a) \(\int\limits^{\dfrac{\pi}{2}}_0\left(x+1\right)\sin x.dx\)
b) \(\int\limits^e_1x^2lnxdx\)
c) \(\int\limits^1_0ln\left(1+x\right)dx\)
d) \(\int\limits^1_0\left(x^2-2x-1\right)e^{-x}dx\)
+∞∫ x (ln^3x)/x dx xét sự hội tụ hay phân kì của tích phân suy rộng0
Đọc tiếp
+∞∫ x (ln^3x)/x dx xét sự hội tụ hay phân kì của tích phân suy rộng
0
Áp dụng phương pháp tính tích phân, hãy tính các tích phân sau :
a) intlimits^{dfrac{pi}{2}}_0xcos2xdx
b) intlimits^{ln2}_0xe^{-2x}dx
c) intlimits^1_0lnleft(2x+1right)dx
d) intlimits^3_2left|lnleft(x-1right)-lnleft(x+1right)right|dx
e) intlimits^2_{dfrac{1}{2}}left(1+x-dfrac{1}{x}right)e^{x+dfrac{1}{x}}dx
g) intlimits^{dfrac{pi}{2}}_0xcos xsin^2xdx
h) intlimits^1_0dfrac{xe^x}{left(1+xright)^2}dx
i) intlimits^e_1dfrac{1+xln x}{x}e^xdx
Đọc tiếp
Áp dụng phương pháp tính tích phân, hãy tính các tích phân sau :
a) \(\int\limits^{\dfrac{\pi}{2}}_0x\cos2xdx\)
b) \(\int\limits^{\ln2}_0xe^{-2x}dx\)
c) \(\int\limits^1_0\ln\left(2x+1\right)dx\)
d) \(\int\limits^3_2\left|\ln\left(x-1\right)-\ln\left(x+1\right)\right|dx\)
e) \(\int\limits^2_{\dfrac{1}{2}}\left(1+x-\dfrac{1}{x}\right)e^{x+\dfrac{1}{x}}dx\)
g) \(\int\limits^{\dfrac{\pi}{2}}_0x\cos x\sin^2xdx\)
h) \(\int\limits^1_0\dfrac{xe^x}{\left(1+x\right)^2}dx\)
i) \(\int\limits^e_1\dfrac{1+x\ln x}{x}e^xdx\)
Tính tích phân của hàm số chứa Ln:
\(I=\int_{\varepsilon}^{\varepsilon^2}\left(\frac{1}{\ln^2x}-\frac{1}{\ln x}\right)dx\)
MỌI NGƯỜI GIÚP MÌNH CÂU TÍCH PHÂN NÀY VỚI!!!!!!!!
Tích phân từ 0 đến π/4 của xsin(x)dxGiúp em với ạ
Xem chi tiết
tính tích phân của tanx.dx cận từ π/4 đến -π/4
ai giúp mình với. mình đang gấp ạ
Xét sự hội tụ của tích phân suy rộng sau:
I =\(\int\limits^{+\infty}_0\dfrac{x+1}{\left(x^2+1\right)\sqrt{x^3+1}}dx\)
tính tích phân 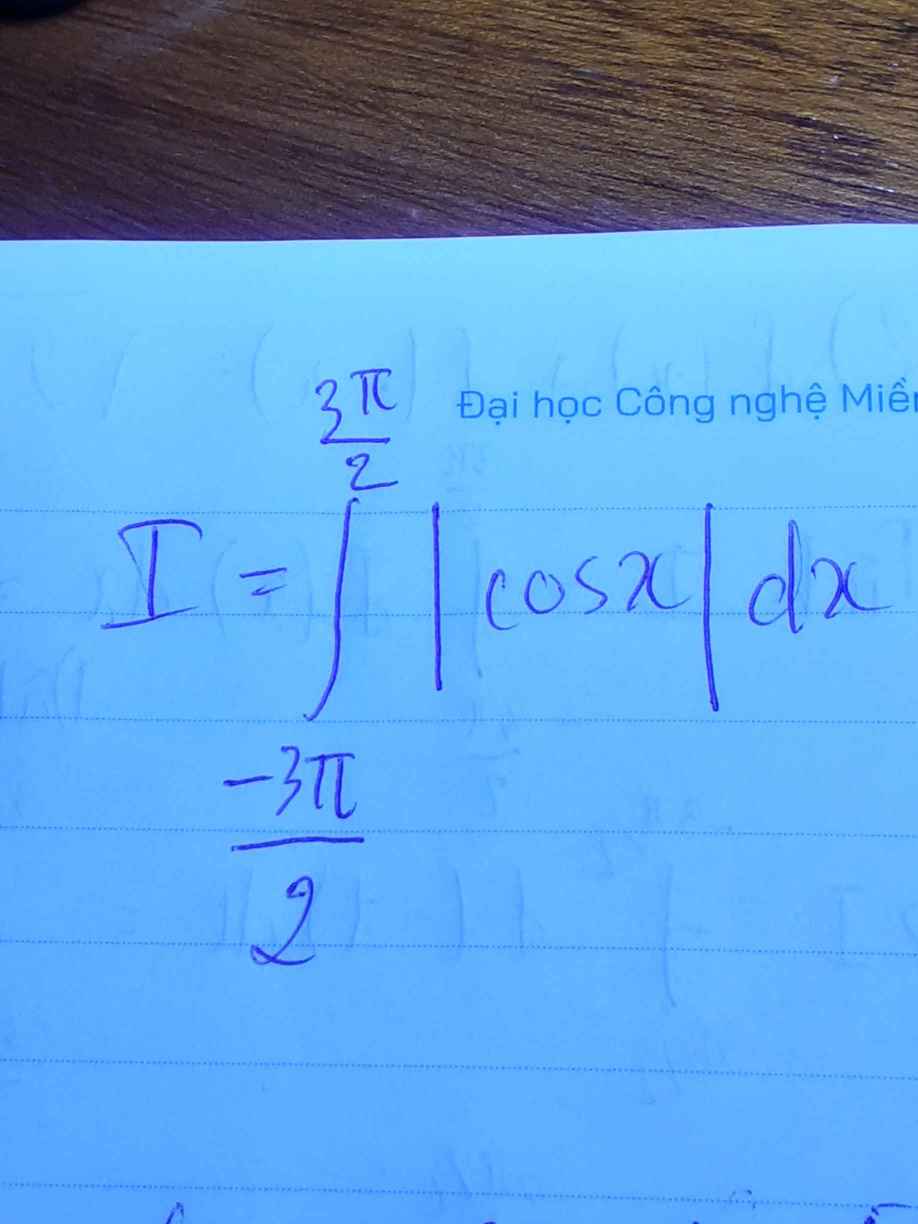
Tính tích phân