Hướng dẫn:
Điểm M thuộc đường trung trực của AB
=> MA = MB (định lí thuận)
Vì MA = 5cm nên MB = 5cm
Hướng dẫn:
Điểm M thuộc đường trung trực của AB
=> MA = MB (định lí thuận)
Vì MA = 5cm nên MB = 5cm
Hướng dẫn:
Điểm M thuộc đường trung trực của AB
=> MA = MB (định lí thuận)
Vì MA = 5cm nên MB = 5cm
Hướng dẫn:
Điểm M thuộc đường trung trực của AB
=> MA = MB (định lí thuận)
Vì MA = 5cm nên MB = 5cm
tính độ dài điểm M nằm trên đường trung trực d của đoạn thẳng AB, biết MA=7cm
1,Điểm M nằm trên đường trung trực của đoạn thẳng AB,Biết MB=3cm.Hỏi độ dài đoạn thẳng MA=?
2,Biết diểm C,D cùng nằm trên đường trung trực của AB.Chứng tỏ góc CBD=gócCAD?
3,Hai điểm M,N nằm trên môt nửa mặt phẳng có bờ là đường thẳng xy.Lấy điểm P đối xứng với M qua xy,gọi I là một điểm thuộc xy.Hãy so sánh IM+IN với PN ?
Cho góc nhọn xOy và điểm M nằm trong góc ấy. Từ M kẻ các đường vuông góc MA , MB lần lượt xuống Ox và Oy. Gọi C là trung điểm của đoạn thẳng OM, P là trung điểm đoạn thẳng AB. Chứng minh rằng CP là trung trực của tam giác ABC
cho 2 đường thẳng xx' và yy' cắt nhau tại O. Trên tia Ox lấy 2 điểm A,B sao cho A nằm giữa B, AB= 2OA.Trên yy' lấy 2 điểm L và M sao cho O là trung điểm của LM.Nối B với L, B với M và gọi P là trung điểm của đoạn MB,Q là trung điểm của đoạn LB. Chứng minh rằng các đoạn thẳng LP và MQ đi qua A.
Cho hình 12, M là một điểm tùy ý nằm trên đường thẳng a. Vẽ điểm C sao cho a là đường trung trực của AC
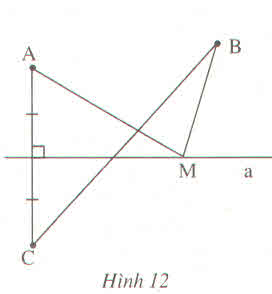
a) Hãy so sánh MA + MB với BC
b) Tìm vị trí của điểm M trên đường thẳng a để MA + MB là nhỏ nhất ?
Cho đoạn thẳng AB có trung điểm M. Tập hợp các điểm C sao cho tam giác ABC là tam giác cân có đáy là AB là:
đường trung trực của AB.
một đường thẳng đi qua trung điểm M của AB, không lấy điểm M.
một đường thẳng đi qua trung điểm M của AB.
đường trung trực của AB, không lấy trung điểm M của AB.
Cho hai điểm M, N nằm trên đường trung trực của đoạn thẳng AB
Chứng minh \(\Delta AMN=\Delta BMN\)
Cho hai điểm M, N nằm trên đường trung trực của đoạn thẳng AB
Chứng minh \(\Delta AMN=\Delta BMN\)
Cho hai điểm M, N nằm trên đường trung trực của đoạn thẳng AB
Chứng minh \(\Delta AMN=\Delta BMN\)