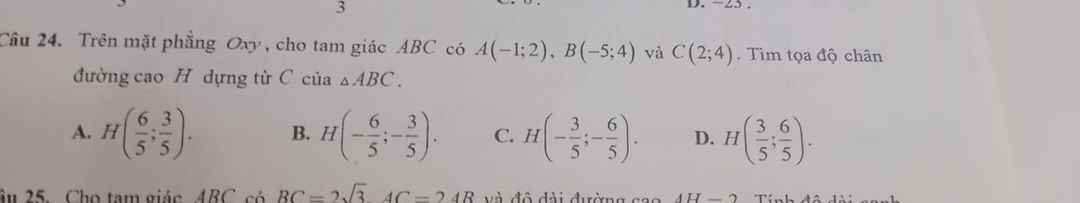4. co \(\overrightarrow{CB}\cdot\overrightarrow{CA}=0\)
-12+(4-m)(3-m)=0
\(\Rightarrow\left[\begin{matrix}m=7\\m=0\end{matrix}\right.\)
5. trong tam G(1;3)
truc tam H
\(\left\{\begin{matrix}AH\perp BC\\B,H,Cthanghang\end{matrix}\right.\)
\(\left\{\begin{matrix}\overrightarrow{AH}\cdot\overrightarrow{BC}=0\\BH=kBC\end{matrix}\right.\)
\(\left\{\begin{matrix}6\left(x-1\right)-2\left(y-3\right)=0\\\frac{x+2}{6}=\frac{y-4}{-2}\end{matrix}\right.\)
\(\left\{\begin{matrix}x=1\\y=3\end{matrix}\right.\)
tam duong tron ngoai tiep I
IA2=IB2=IC2
bạn tính độ dài từng cái \(\left\{\begin{matrix}IA^2=IB^2\\IB^2=IC^2\end{matrix}\right.\)
=> X, Y
7. = \(\left(\overrightarrow{AB}-\overrightarrow{BC}\right)\left(\overrightarrow{AB}+\overrightarrow{BC}\right)+\left(\overrightarrow{CD}-\overrightarrow{DA}\right)\left(\overrightarrow{CD}+\overrightarrow{DA}\right)\)=\(\left(\overrightarrow{AB}-\overrightarrow{BC}\right)\overrightarrow{AC}+\overrightarrow{CA}\left(\overrightarrow{CD}-\overrightarrow{DA}\right)\)
=\(\overrightarrow{AC}\left(\overrightarrow{AB}-\overrightarrow{BC}-\overrightarrow{CD}+\overrightarrow{DA}\right)\)
=\(\overrightarrow{AC}\left(\overrightarrow{DB}-\overrightarrow{BD}\right)=2\overrightarrow{AC}\overrightarrow{DB}\)
7.b)
vi tu giac ABCD co 2 duong cheo vuong goc
=>\(\overrightarrow{AC}\overrightarrow{DB}=0\)
TA CO \(AB^2+CD^2=2\overrightarrow{AC}\cdot\overrightarrow{DB}+BC^2+AD^2\)
\(\Leftrightarrow AB^2+CD^2=BC^2+AD^2\)