1) \(B=\dfrac{1}{\sqrt{x}-2}-\dfrac{\sqrt{x}}{4-x}=\dfrac{1}{\sqrt{x}-2}+\dfrac{\sqrt{x}}{x-4}=\dfrac{1}{\sqrt{x}-2}+\dfrac{\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)\(=\dfrac{\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\dfrac{\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{2\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{2\sqrt{x}+2}{x-4}\)
Thay \(x=16\) vào biểu thức B ta được :
\(B=\dfrac{2\sqrt{x}+2}{x-4}=\dfrac{2\sqrt{16}+2}{16-4}=\dfrac{2\cdot4+2}{12}=\dfrac{10}{12}=\dfrac{5}{6}\)
2) \(P=\dfrac{B}{A}=\dfrac{\dfrac{2\sqrt{x}+2}{x-4}}{\dfrac{2}{\sqrt{x}+2}}=\dfrac{2\sqrt{x}+2}{x-4}\cdot\dfrac{\sqrt{x}+2}{2}=\dfrac{2\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)\cdot2}=\dfrac{\sqrt{x}+1}{\sqrt{x}-2}\)
3)
\(P< 1\Rightarrow\dfrac{\sqrt{x}+1}{\sqrt{x}-2}< 1\)
\(\Rightarrow\dfrac{\sqrt{x}+1}{\sqrt{x}-2}-1< 0\)
\(\Rightarrow\dfrac{\sqrt{x}+1-\left(\sqrt{x}-2\right)}{\sqrt{x}-2}< 0\)
\(\Rightarrow\dfrac{\sqrt{x}+1-\sqrt{x}+2}{\sqrt{x}-2}< 0\)
\(\Rightarrow\dfrac{3}{\sqrt{x}-2}< 0\)
\(\Rightarrow\sqrt{x}-2< 0\)
\(\Rightarrow\sqrt{x}< 2\)
\(\Rightarrow x< 4\Rightarrow x\in\left\{0;1;2;3\right\}\)






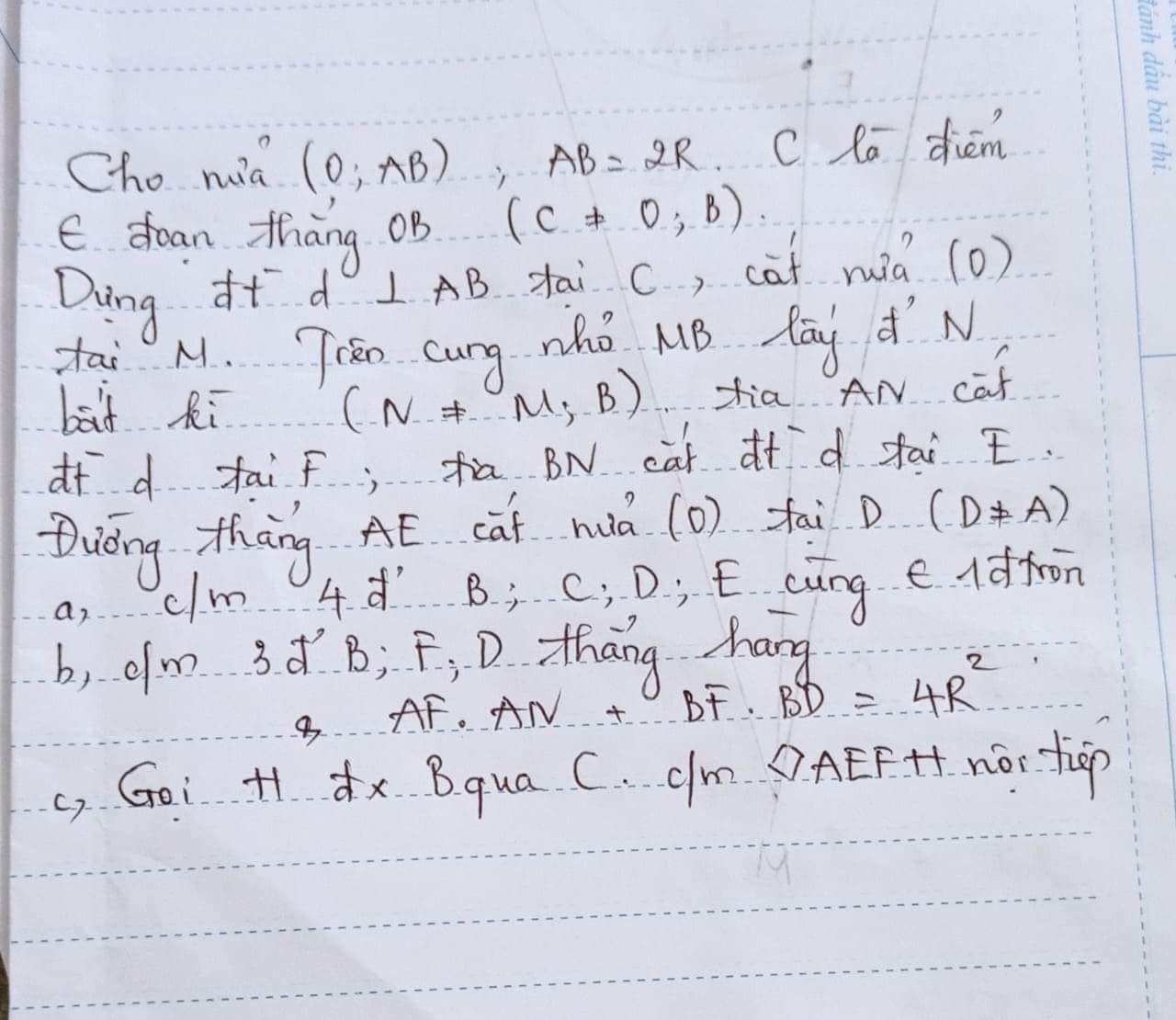






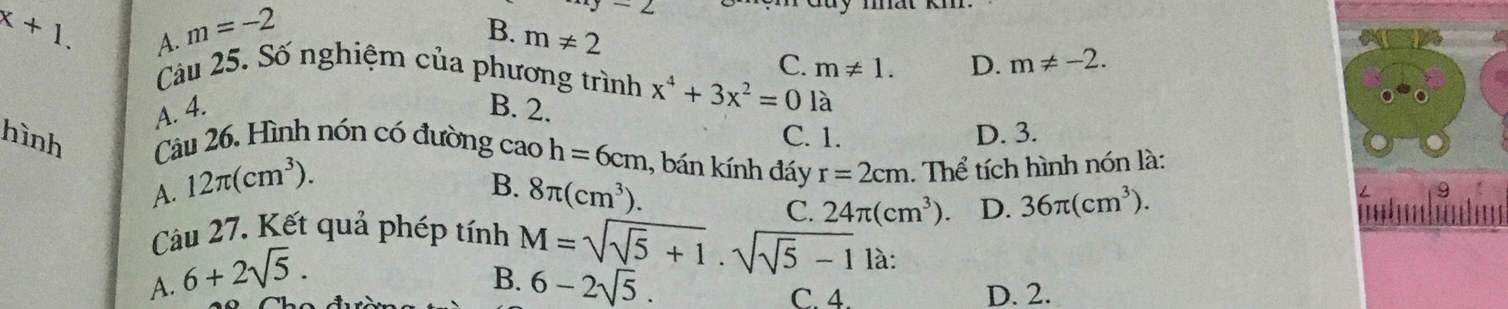

 Giúp mình với ạ , mai mk bộp bài rùi :
Giúp mình với ạ , mai mk bộp bài rùi :