a, Tổng số bi là : 6+5+4 = 15 viên .
=> Chọn bất kì có : \(C^4_{15}=1365\) cách.
b, Có đúng 2 bi xanh và 2 bi vàng : \(C^2_6.C^2_4\) = 90 cách.
c, Có đủ cả 3 màu ta có:
TH1: 1 xanh, 1 đỏ, 2 vàng có : \(C^1_6.C^1_5.C^2_4=180\) cách.
TH2 : 2 xanh, 1 đỏ, 1 vàng có : \(C^2_6.C^1_5.C^1_4=300\) cách.
TH3: 1 xanh, 2 đỏ, 1 vàng có : \(C^1_6.C^2_5.C^1_4=240\) cách.
Vậy ta có tổng là : 180 + 300 + 240 = 720 cách.
d, Số bi xanh và số bi đỏ bằng nhau nên ta có: 2 xanh và 2 đỏ.
=> Số cách chọn là: \(C^2_6.C^2_5=150\) cách.
e, Có ít nhất 1 viên bi xanh nên ta có phủ định là không có viên bi xanh nào nên chọn 2 đỏ và 2 vàng: \(C^2_5.C^2_4=60\) cách.
Vậy số cách chọn ít nhất 1 xanh là: 1365 - 60 = 1305 cách
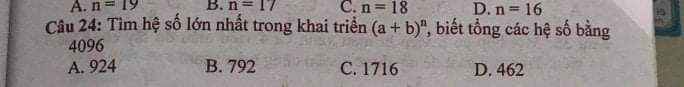
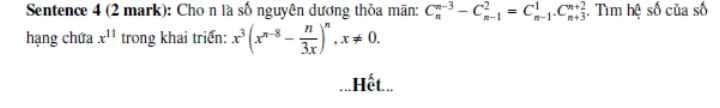
giúp mình với ạ