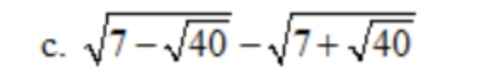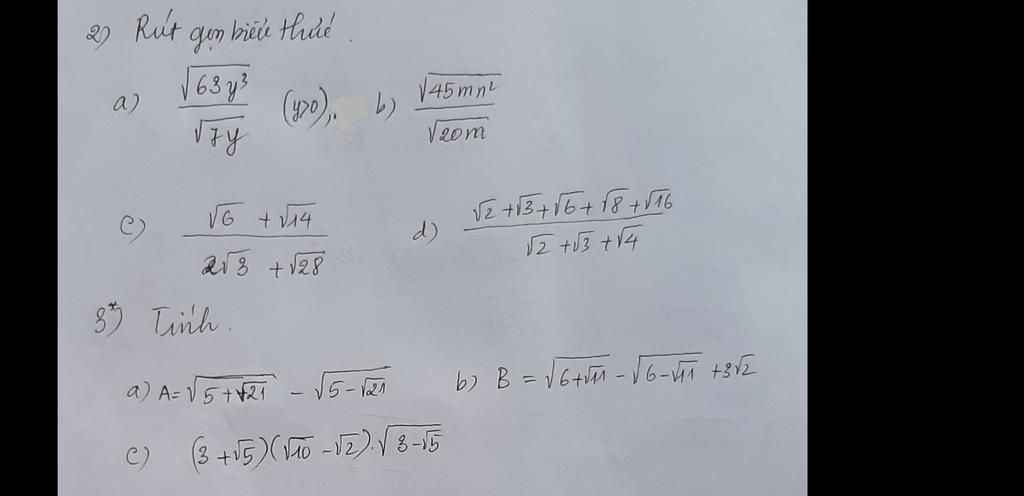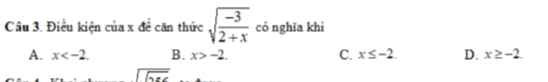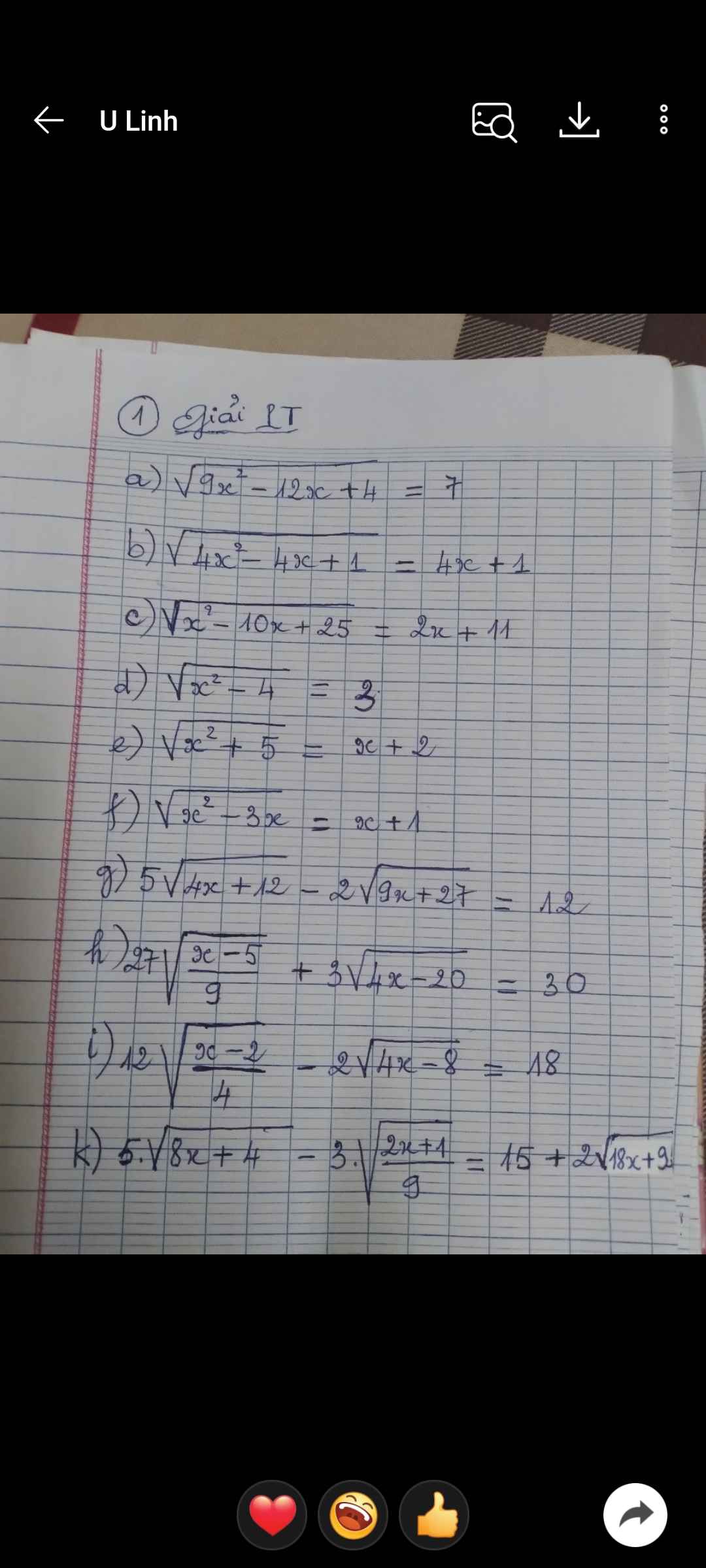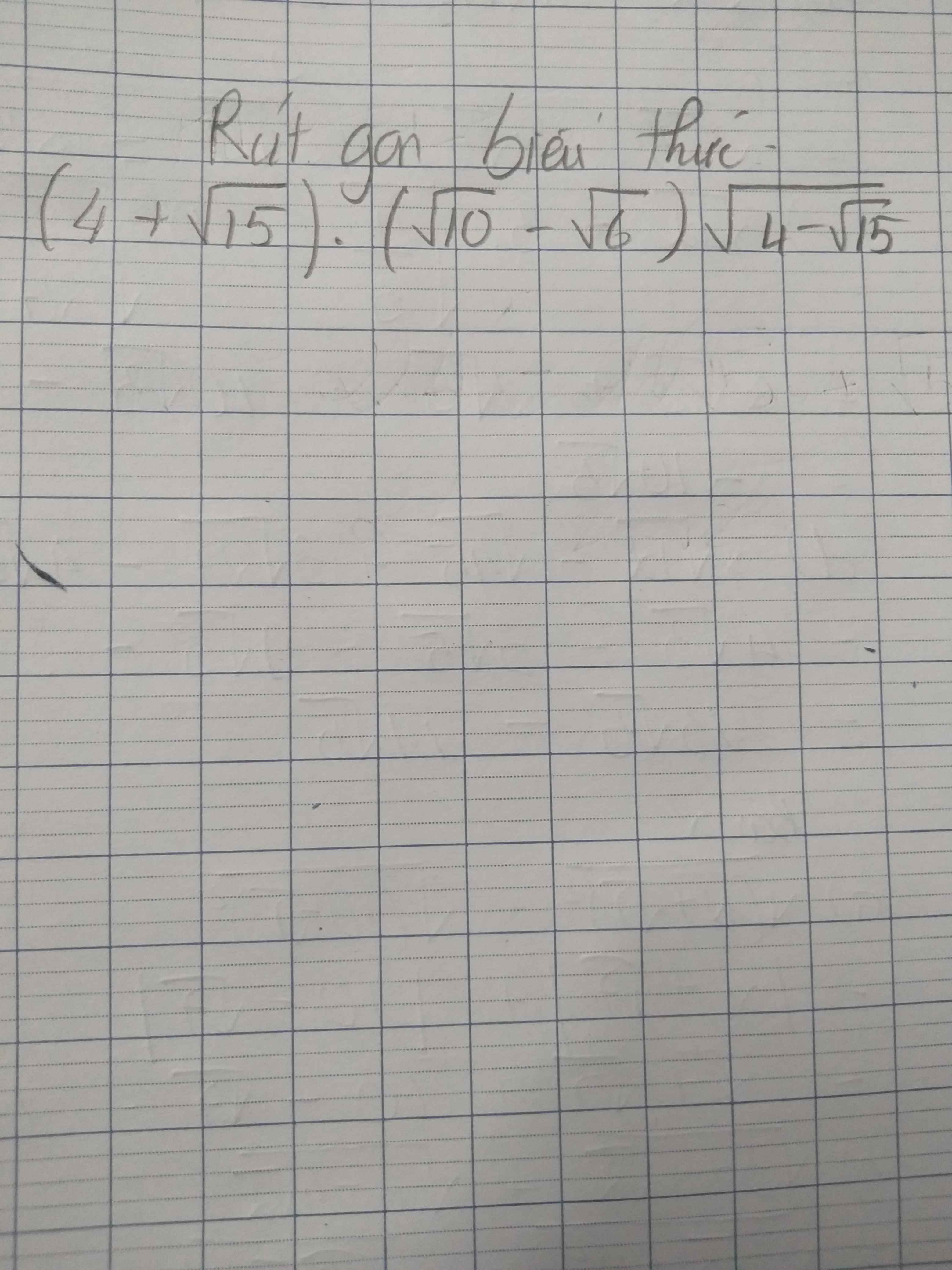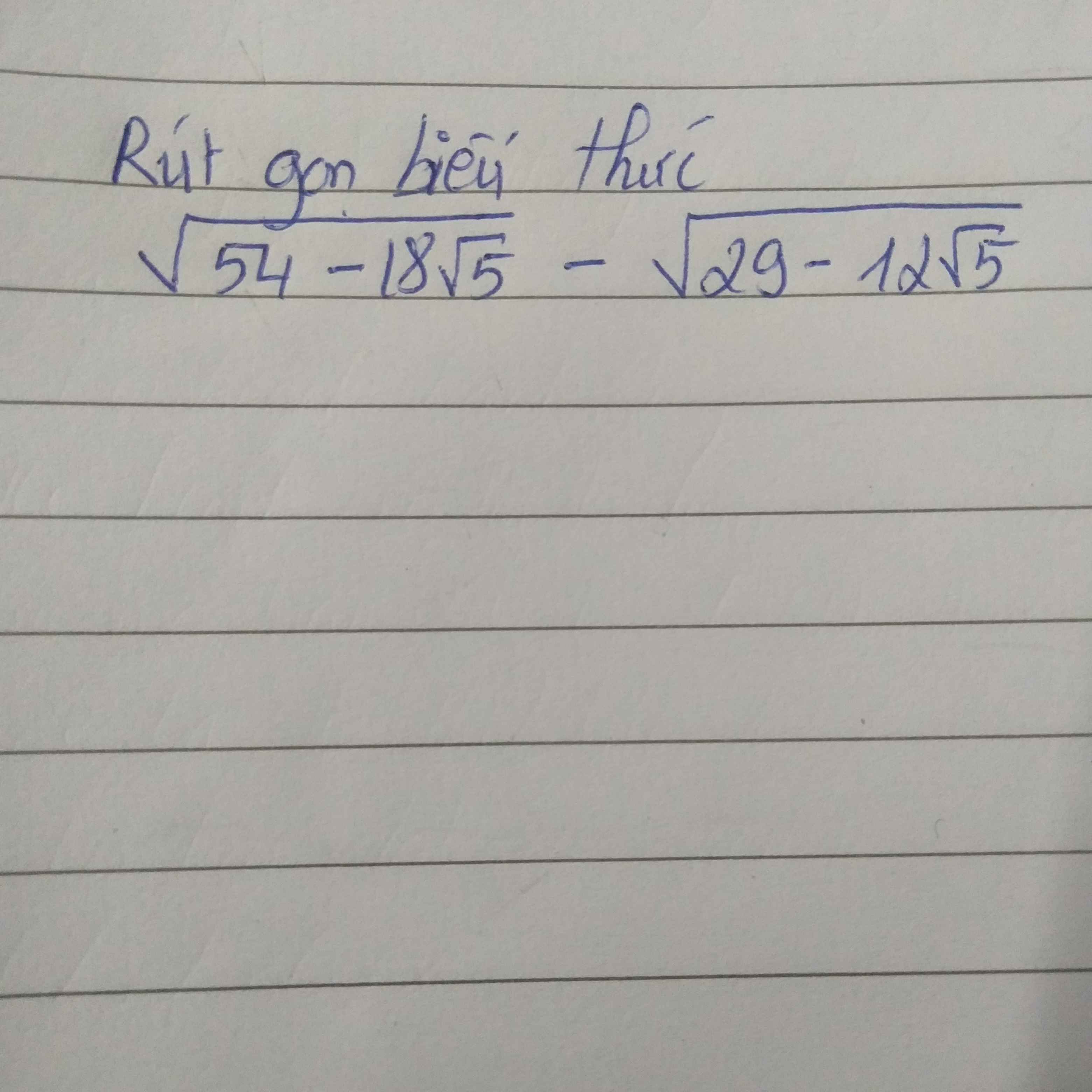c) \(=\sqrt{7-2\sqrt{10}}-\sqrt{7+\sqrt{40}}\)
\(=\sqrt{\left(\sqrt{5}-\sqrt{2}\right)^2}-\sqrt{\left(\sqrt{5}+\sqrt{2}\right)^2}\)
\(=\left|\sqrt{5}-\sqrt{2}\right|-\left|\sqrt{5}+\sqrt{2}\right|\)
\(=\sqrt{5}-\sqrt{2}-\left(\sqrt{5}+\sqrt{2}\right)=-2\sqrt{2}\)
\(=\dfrac{\left(\sqrt{14-2\sqrt{40}}-\sqrt{14+2\sqrt{40}}\right)}{\sqrt{2}}=\dfrac{\left|\sqrt{10}-2\right|-\left|\sqrt{10}+2\right|}{\sqrt{2}}=\dfrac{\sqrt{10}-2-\sqrt{10}-2}{\sqrt{2}}=\dfrac{-4}{\sqrt{2}}=-2\sqrt{2}\)