a: Đặt B=3+5+7+...+49
Số số hạng là (49-3):2+1=24(số)
Tổng là (49+3)*24/2=624
\(A=\dfrac{1}{5}\left(\dfrac{5}{4\cdot9}+\dfrac{5}{9\cdot14}+...+\dfrac{5}{44\cdot49}\right)\cdot\dfrac{1-624}{89}\)
\(=\dfrac{1}{5}\cdot\left(\dfrac{1}{4}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{14}+...+\dfrac{1}{44}-\dfrac{1}{49}\right)\cdot\dfrac{-623}{89}\)
\(=-\dfrac{7}{5}\cdot\left(\dfrac{1}{4}-\dfrac{1}{49}\right)=\dfrac{-7}{5}\cdot\dfrac{45}{196}=\dfrac{-9}{28}\)
b: \(=\dfrac{2^{12}\cdot3^5-2^{12}\cdot3^4}{2^{12}\cdot3^6+2^{12}\cdot3^5}-\dfrac{5^{10}\cdot7^3-5^{10}\cdot7^4}{5^9\cdot7^3+5^9\cdot7^3\cdot2^3}\)
\(=\dfrac{2^{12}\cdot3^4\left(3-1\right)}{2^{12}\cdot3^5\left(3+1\right)}-\dfrac{5^{10}\cdot7^3\left(1-7\right)}{5^9\cdot7^3\left(1+2^3\right)}\)
\(=\dfrac{1}{3}\cdot\dfrac{-2}{4}-\dfrac{5\cdot\left(-6\right)}{9}\)
\(=\dfrac{-1}{6}+\dfrac{10}{3}=\dfrac{-1}{6}+\dfrac{20}{6}=\dfrac{19}{6}\)

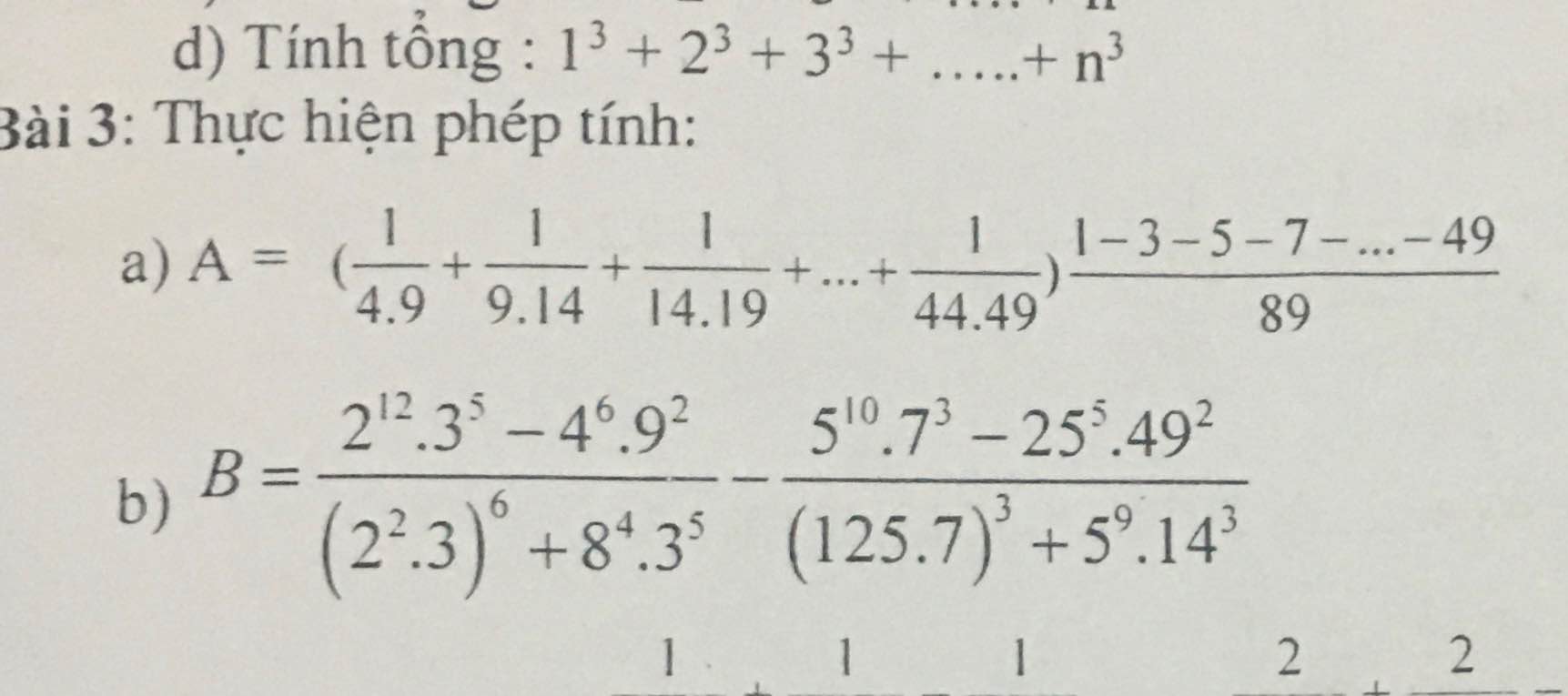




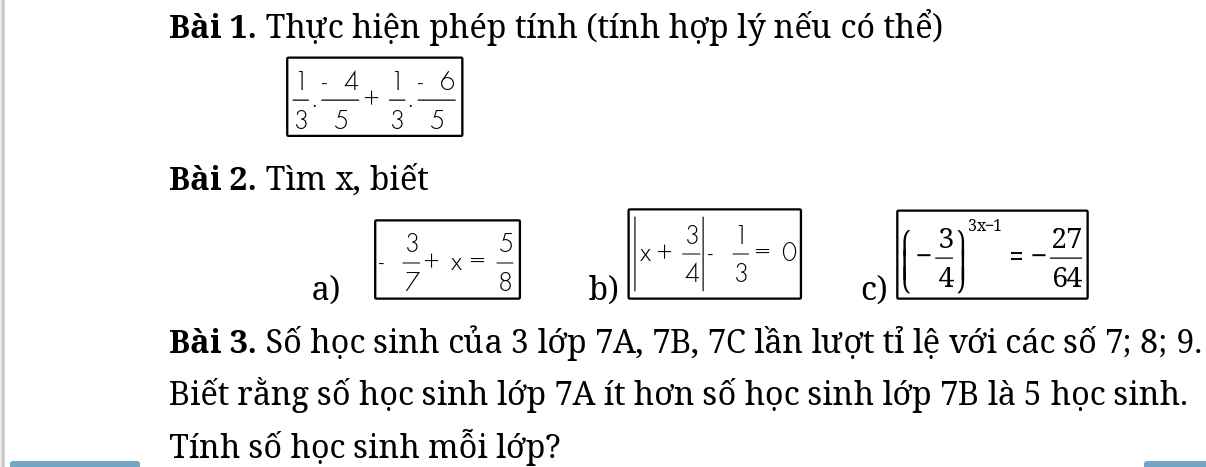 Mọi người ơi , mọi người giúp mình với , mình trân thành cảm ơn
Mọi người ơi , mọi người giúp mình với , mình trân thành cảm ơn
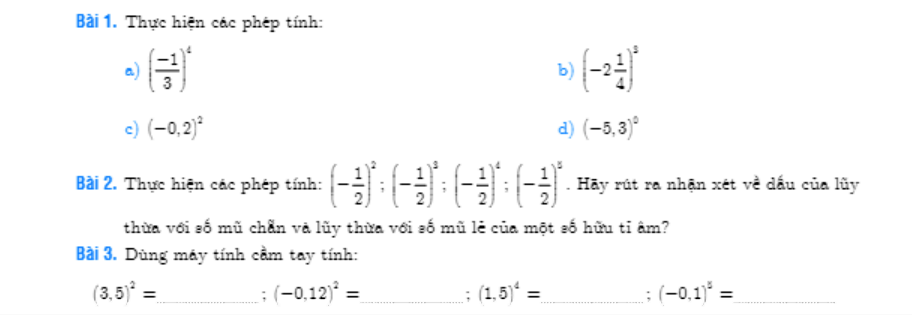


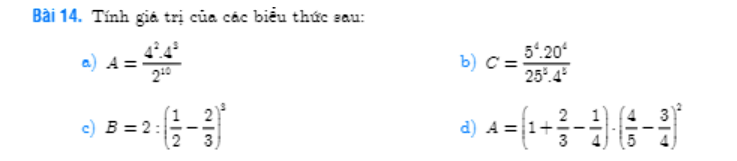



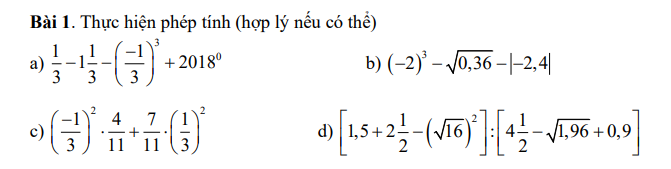


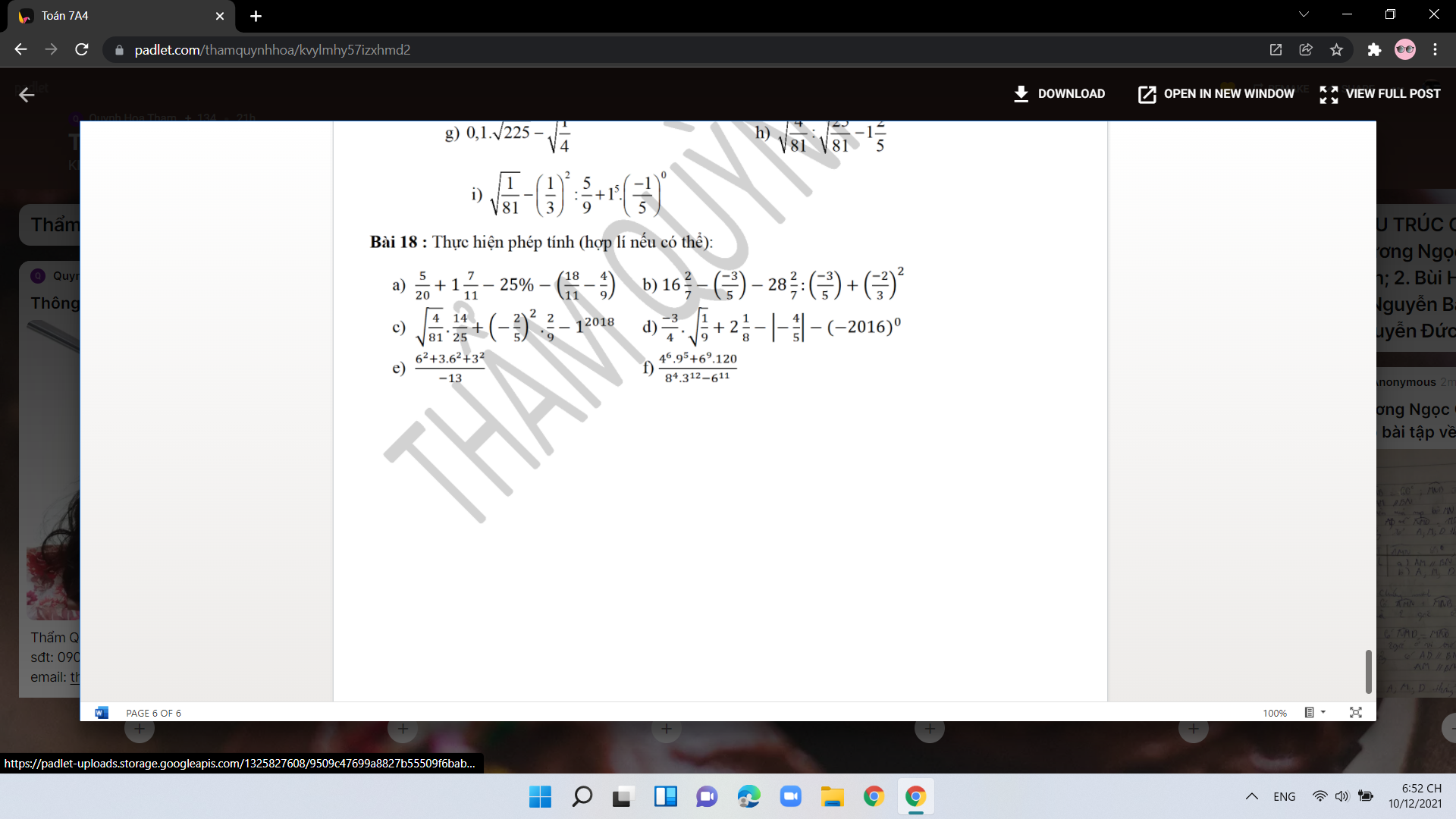 mọi người giúp mình với, mình đang cần gấp
mọi người giúp mình với, mình đang cần gấp