a) \(\dfrac{2x}{3}\)+\(\dfrac{2x-1}{6}\)=4 - \(\dfrac{x}{3}\)
<=>\(\dfrac{2x}{3}\)+\(\dfrac{2x-1}{6}\) - 4+\(\dfrac{x}{3}\)=0
<=>\(\dfrac{2x.2+2x-1-4.6+x.2}{6}\)=0
=>4x-2x-24+2x=0
<=>4x-24=0
<=>4x=24
<=>x=6
Vậy x=6
b)\(\dfrac{x-1}{2}\)+\(\dfrac{x-1}{4}\)=1 - \(\dfrac{2\left(x-1\right)}{3}\)
<=>\(\dfrac{x-1}{2}\)+\(\dfrac{x-1}{4}\)-1+\(\dfrac{2\left(x-1\right)}{3}\)=0
<=>\(\dfrac{6.\left(x-1\right)+3\left(x-1\right)-1.12+4.2\left(x-1\right)}{12}\)=0
=>6x-6+3x-3-12+4x-4+2x-2=0
<=>15x-27=0
<=>15x=27
<=>x=\(\dfrac{9}{5}\)
Vậy x=\(\dfrac{9}{5}\)
d)\(\dfrac{7x}{8}\)-5(x-9)=20x+\(\dfrac{1,5}{6}\)
<=>\(\dfrac{7x}{8}\)-5(x-9)-20x-\(\dfrac{1,5}{6}\)=0
<=>\(\dfrac{3.7x-24.5\left(x-9\right)-20x.24-1,5.4}{24}\)=0
=>-478x+165=0
<=> - 478= - 165
<=> x=\(\dfrac{165}{487}\)
Vậy x =\(\dfrac{165}{487}\)
c) \(\dfrac{2-x}{2001}\)-1=\(\dfrac{1-x}{2002}\)-\(\dfrac{x}{2003}\)
<=>\(\dfrac{2-x}{2001}\)-1-\(\dfrac{1-x}{2002}\)+\(\dfrac{x}{2003}\)=0
<=>\(\dfrac{2002.2003\left(2-x\right)-1.2001.2002.2003-2001.2003\left(1-x\right)+2001.2002.x}{8024022006}\)=0
=>4004-2002x+4006-2003x-2001-2002-2003-2001+2001x+2003-2003x+2001x+2002x=0
<=>-4x+2006=0
<=>-4x=-2006
<=>x=\(\dfrac{1003}{2}\)
Vậy x=\(\dfrac{1003}{2}\)








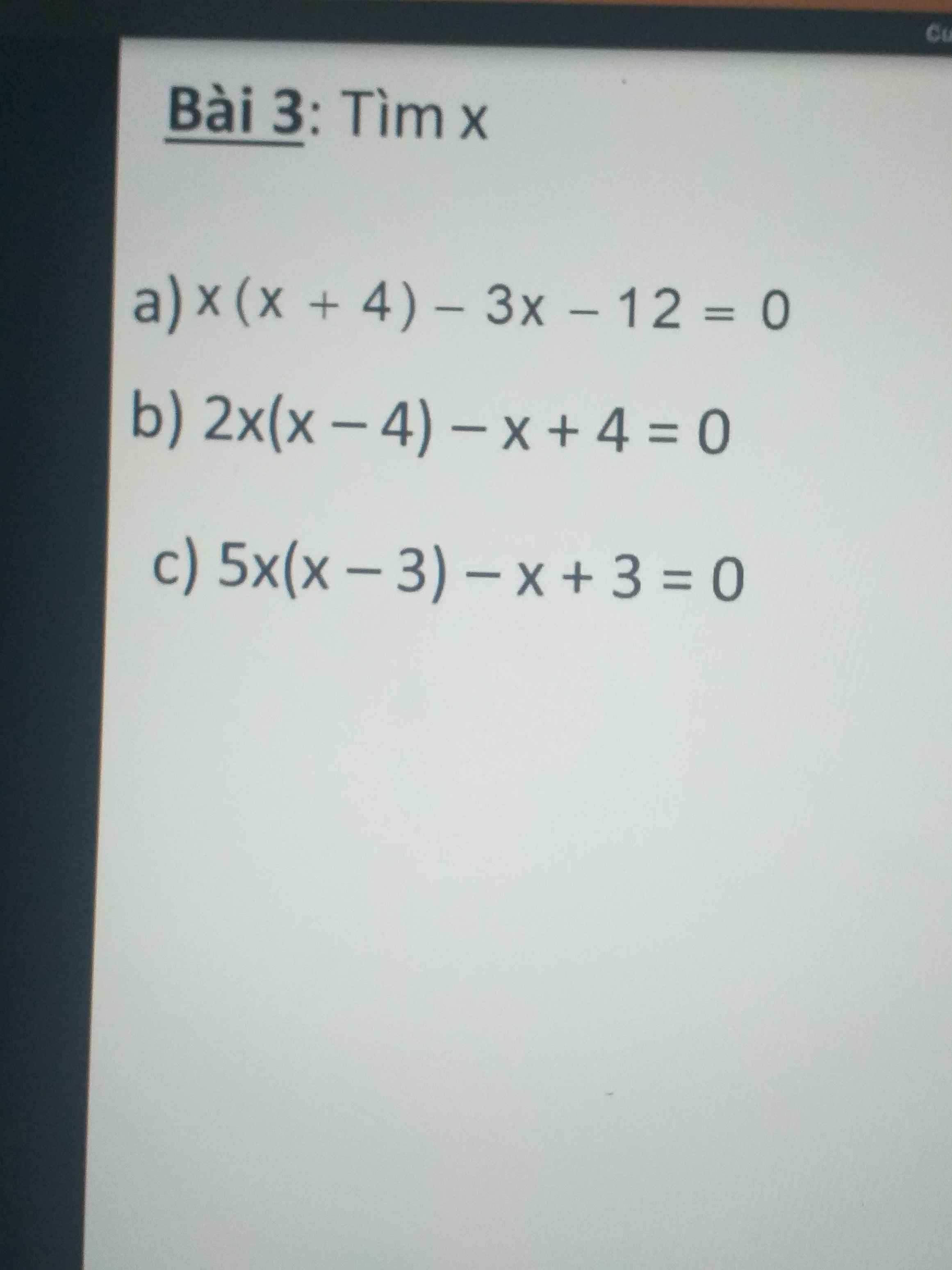


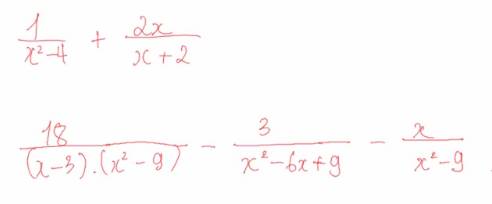
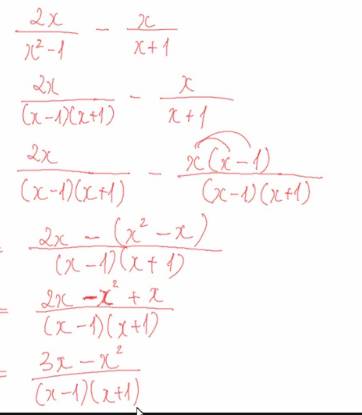



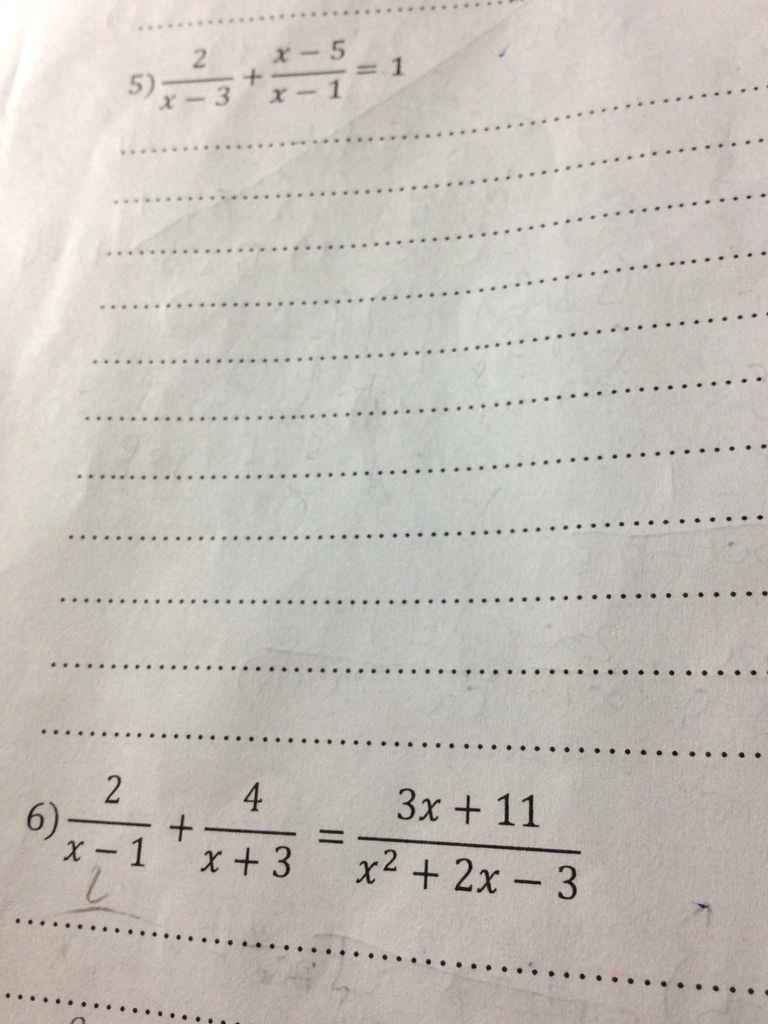 Giúp mình thêm 2 câu này cực gấp luôn nha cảm ơn
Giúp mình thêm 2 câu này cực gấp luôn nha cảm ơn
