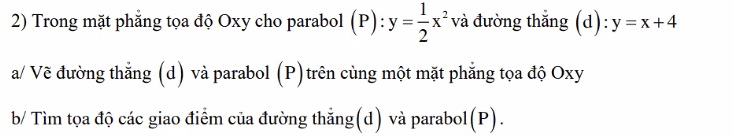Bài 1:
a) \(A=8\sqrt{2}-15\sqrt{3}-8\sqrt{2}+15\sqrt{3}=0\)
b) \(B=\dfrac{\left(5+\sqrt{5}\right)\left(\sqrt{5}-2\right)}{5-4}+\dfrac{\sqrt{5}\left(\sqrt{5}+1\right)}{5-1}-\dfrac{3\sqrt{5}\left(3-\sqrt{5}\right)}{9-5}\)
\(=-5+3\sqrt{5}+\dfrac{5+\sqrt{5}-9\sqrt{5}+15}{4}=-5+3\sqrt{5}+\dfrac{4\left(5-2\sqrt{5}\right)}{4}=-5+3\sqrt{5}+5-2\sqrt{5}=\sqrt{5}\)
c) \(C=\sqrt{7}-2-\sqrt{7}=-2\)
Bài 2:
ĐKXĐ: \(x\ge2,x\ne4\)
a) \(A=\dfrac{x+2\sqrt{x}+x-2\sqrt{x}-x+2\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}}{\sqrt{x}-2}\)
b) \(A=\dfrac{\sqrt{x}}{\sqrt{x}-2}>\dfrac{1}{3}\)
\(\Leftrightarrow3\sqrt{x}>\sqrt{x}-2\Leftrightarrow\sqrt{x}>-1\left(đúng\forall x\right)\)
c) \(A=\dfrac{\sqrt{x}}{\sqrt{x}-2}=1+\dfrac{2}{\sqrt{x}-2}\in Z\)
\(\Leftrightarrow\sqrt{x}-2\inƯ\left(2\right)=\left\{-2;-1;1;2\right\}\)
Kết hợp ĐKXĐ:
\(\Leftrightarrow x\in\left\{0;1;9;16\right\}\)

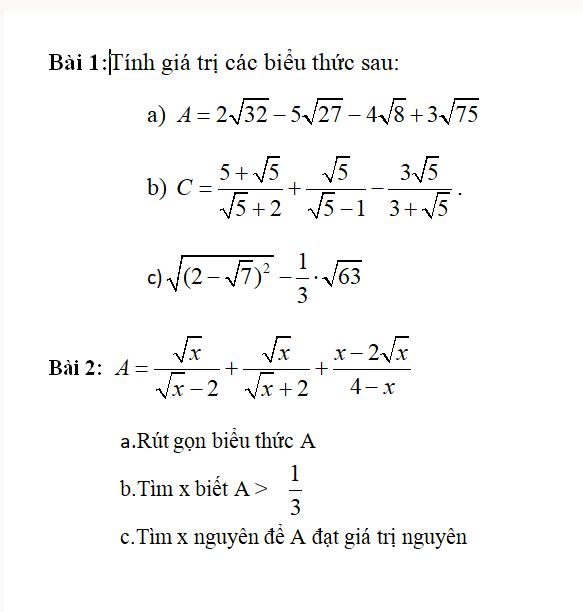 giup mik voi pleeee
giup mik voi pleeee