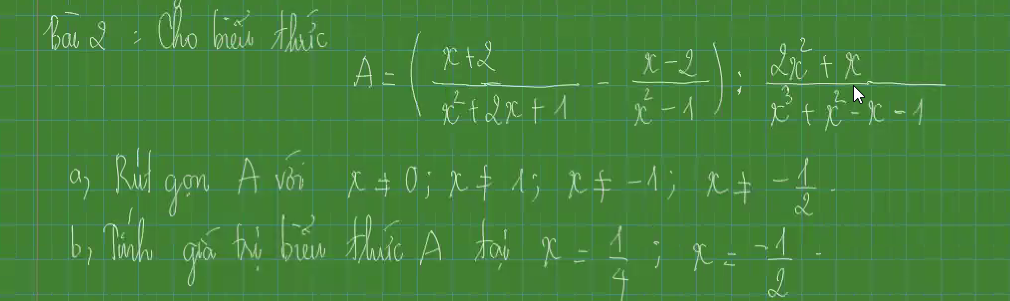a) Ta có: \(\dfrac{x^4+4}{x\left(x^2+2\right)-2x^2-\left(x-1\right)^2-1}\)
\(=\dfrac{x^4+4x^2+4-4x^2}{x^3+2x-2x^2-x^2+2x-1-1}\)
\(=\dfrac{\left(x^2+2\right)^2-\left(2x\right)^2}{x^3-3x^2+4x-2}\)
\(=\dfrac{\left(x^2-2x+2\right)\left(x^2+2x+2\right)}{x^3-x^2-2x^2+2x+2x-2}\)
\(=\dfrac{\left(x^2-2x+2\right)\left(x^2+2x+2\right)}{x^2\left(x-1\right)-2x\left(x-1\right)+2\left(x-1\right)}\)
\(=\dfrac{\left(x^2-2x+2\right)\left(x^2+2x+2\right)}{\left(x-1\right)\left(x^2-2x+2\right)}\)
\(=\dfrac{x^2+2x+2}{x-1}\)(đpcm)
b) Ta có: \(\dfrac{x^2+y^2-z^2-2zt+2xy-t^2}{x^2-y^2+z^2-2yt+2xz-t^2}\)
\(=\dfrac{\left(x^2+2xy+y^2\right)-\left(z^2+2zt+t^2\right)}{\left(x^2+2xz+z^2\right)-\left(y^2+2yt+t^2\right)}\)
\(=\dfrac{\left(x+y\right)^2-\left(z+t\right)^2}{\left(x+z\right)^2-\left(y+t\right)^2}\)
\(=\dfrac{\left(x+y-z-t\right)\left(x+y+z+t\right)}{\left(x+z-y-t\right)\left(x+z+y+t\right)}\)
\(=\dfrac{x+y-z-t}{x-y+z-t}\)
c) Ta có: \(\dfrac{3y-2-3xy+2x}{1-3x-x^3+3x^2}\)
\(=\dfrac{\left(3y-2\right)-x\left(3y-2\right)}{\left(1-x\right)\left(1+x+x^2\right)-3x\left(1-x\right)}\)
\(=\dfrac{\left(3y-2\right)\left(1-x\right)}{\left(1-x\right)\left(x^2+x+1-3x\right)}\)
\(=\dfrac{3y-2}{x^2-2x+1}\)
\(=\dfrac{3y-2}{\left(1-x\right)^2}\)

 Giúp em vs ạ
Giúp em vs ạ



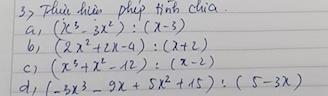

 bài 7 . 8 làm giúp mil vs ạ mik đg vội
bài 7 . 8 làm giúp mil vs ạ mik đg vội