a) Ta có: \(\angle AHD+\angle AKD=90+90=180\Rightarrow AHDK\) nội tiếp
Vì \(\Delta ADB\) vuông tại D có \(DH\bot AB\Rightarrow AD^2=AH.AB\)
Vì \(\Delta ADC\) vuông tại D có \(DK\bot AC\Rightarrow AD^2=AK.AC\)
\(\Rightarrow AH.AB=AK.AC\)
b) \(AH.AB=AK.AC\Rightarrow\dfrac{AH}{AK}=\dfrac{AC}{AB}\)
Xét \(\Delta AHK\) và \(\Delta ACB:\) Ta có: \(\left\{{}\begin{matrix}\angle BACchung\\\dfrac{AH}{AK}=\dfrac{AC}{AB}\end{matrix}\right.\)
\(\Rightarrow\Delta AHK\sim\Delta ACB\left(c-g-c\right)\Rightarrow\angle AHK=\angle ACB\)
\(\Rightarrow BHKC\) nội tiếp \(\Rightarrow\angle AKH=\angle ABC\)
Ta có: \(\angle OAC=\dfrac{180-\angle AOC}{2}=90-\dfrac{1}{2}\angle AOC=90-\angle ABC\)
\(\Rightarrow\angle OAC+\angle AKH=90\Rightarrow OA\bot HK\)
c) HK cắt DE tại M
Ta có: \(\angle AEB=\angle ADB=90\Rightarrow AEDB\) nội tiếp
\(\Rightarrow\angle CED=\angle ABC\)
BHKC nội tiếp \(\Rightarrow\angle AKH=\angle ABC\)
\(\Rightarrow\angle FKE=\angle FEK\Rightarrow\Delta FEK\) cân tại F \(\Rightarrow FE=FK\)
mà \(\Delta DKE\) vuông tại K \(\Rightarrow F\) là trung điểm 
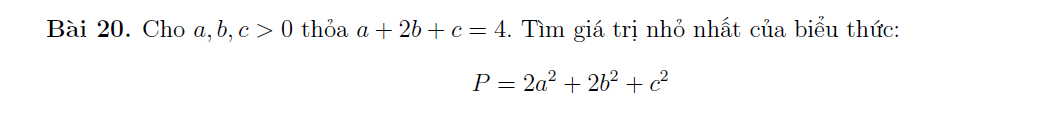
Mọi người ơi,giúp em bài với ạ em cảm ơn ạ
