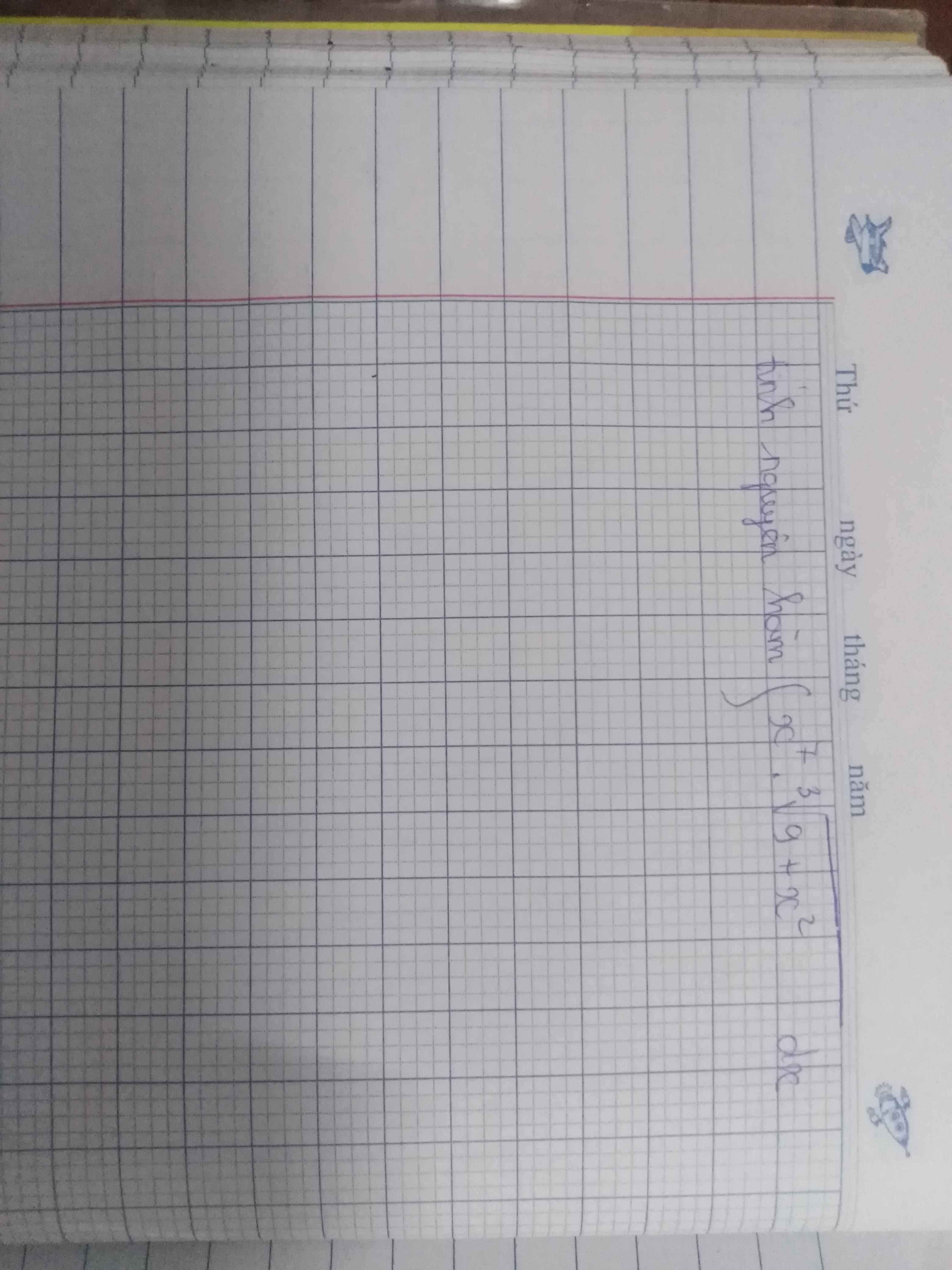
\(I=\int x^6\sqrt[3]{9+x^2}.xdx\)
Đặt \(\sqrt[3]{9+x^2}=t\Rightarrow x^2=t^3-9\)
\(\Rightarrow2x.dx=3t^2dt\Rightarrow x.dx=\dfrac{3}{2}t^2.dt\)
\(\Rightarrow I=\int\left(t^3-9\right)^3.t.\dfrac{3}{2}.t^2dt=\dfrac{3}{2}\int t^3\left(t^3-9\right)^3dt\)
\(=\dfrac{3}{2}\int\left(t^{12}-27t^9+243t^6-729t^3\right)dt\)
\(=\dfrac{3}{2}\left(\dfrac{t^{13}}{13}-\dfrac{27t^{10}}{10}+\dfrac{243t^7}{7}-\dfrac{729t^4}{4}\right)+C\)
\(=\dfrac{3}{2}\left(\dfrac{1}{13}\sqrt[3]{\left(9+x^2\right)^{13}}-\dfrac{27}{10}.\sqrt[3]{\left(9+x^2\right)^{10}}+\dfrac{243}{7}.\sqrt[3]{\left(9+x^2\right)^7}-\dfrac{729}{4}.\sqrt[3]{\left(9+x^2\right)^4}\right)+C\)