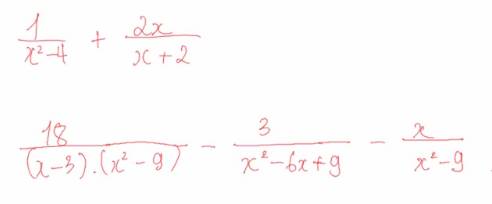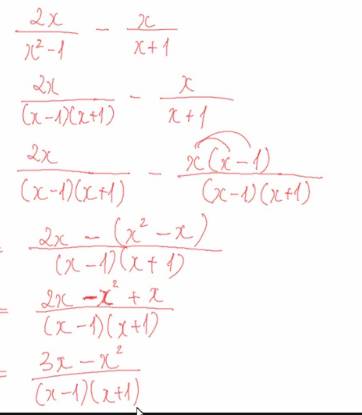giup em bai 1 cau c,d v
1c.
\(\Leftrightarrow\dfrac{x-1991}{9}-1+\dfrac{x-1993}{7}-1+...=\dfrac{x-9}{1991}-1+\dfrac{x-7}{1993}-1+...\) (dài quá làm biếng ghi hết, em cứ hiểu là trừ mỗi số hạng 2 vế cho 1)
\(\Leftrightarrow\dfrac{x-2000}{0}+\dfrac{x-2000}{7}+\dfrac{x-2000}{5}+\dfrac{x-2000}{3}+\dfrac{x-2000}{1}=\dfrac{x-2000}{1991}+\dfrac{x-2000}{1993}+\dfrac{x-2000}{1005}+\dfrac{x-2000}{1997}+\dfrac{x-2000}{1999}\)
\(\Leftrightarrow\left(x-2000\right)\left(\dfrac{1}{9}+\dfrac{1}{7}+\dfrac{1}{5}+\dfrac{1}{3}+1-\dfrac{1}{1991}-\dfrac{1}{1993}-\dfrac{1}{1995}-\dfrac{1}{1997}-\dfrac{1}{1999}\right)=0\)
\(\Leftrightarrow x=2000\)
(do \(\dfrac{1}{9}+\dfrac{1}{7}+\dfrac{1}{5}+\dfrac{1}{3}+1-\dfrac{1}{1991}-\dfrac{1}{1993}-\dfrac{1}{1995}-\dfrac{1}{1997}-\dfrac{1}{1999}\ne0\))
d.
\(\dfrac{x-85}{15}+\dfrac{x-74}{13}+\dfrac{x-67}{11}+\dfrac{x-64}{9}=10\)
\(\Leftrightarrow\dfrac{x-85}{15}-1+\dfrac{x-74}{13}-2+\dfrac{x-67}{11}-3+\dfrac{x-64}{9}-4=0\)
\(\Leftrightarrow\dfrac{x-100}{15}+\dfrac{x-100}{13}+\dfrac{x-100}{11}+\dfrac{x-100}{9}=0\)
\(\Leftrightarrow\left(x-100\right)\left(\dfrac{1}{15}+\dfrac{1}{13}+\dfrac{1}{11}+\dfrac{1}{9}\right)=0\)
\(\Leftrightarrow x=100\)
(do \(\dfrac{1}{15}+\dfrac{1}{13}+\dfrac{1}{11}+\dfrac{1}{9}\ne0\))
2.
\(A=\dfrac{x-1}{x+1}=\dfrac{x+1-2}{x+1}=1-\dfrac{2}{x+1}\)
Do 1 nguyên nên A nguyên khi \(\dfrac{2}{x+1}\) nguyên
\(\Rightarrow x+1=Ư\left(2\right)=\left\{-2;-1;1;2\right\}\)
\(\Rightarrow x=\left\{-3;-2;0;1\right\}\)
Kết hợp ĐKXĐ \(\Rightarrow x=\left\{-3;-2;0\right\}\)
