x2 + x + m - 2 = 0
a) thay m = 0 ta có phương trình:
x2 + x - 2 = 0 ( ta thấy a + b + c = 0 )
=> \(\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
b)
xét delta có
1 - m + 2 = 3-m
để phương trình có 2 nghiệm phân biệt x1;x2 thì delta > 0
=> 3-m > 0
=> m <3
theo Vi-ét ta có:
\(\left\{{}\begin{matrix}x1+x2=-1\\x1x2=m-2\end{matrix}\right.\)
theo bài ra ta có:
x12 + 2x1x2 - x2 = 1
ta có x1 là nghiệm của phương trình x2 + x + m - 2
=> x12 + x1 + m - 2 = 0
=> x12 = 2 - m - x1
=> 2 - m - x1 + 2x1x2 - x2 = 1
=> -(x1+x2) + 2x1x2 - m + 1 = 0
<=> 1 + 2m - 4 - m + 1 = 0
<=> m = 2 ( thỏa điều kiện )
vậy m = 2 để phương trình có 2 nghiệm x1;x2 thỏa mãn x12 + 2x1x2 - x2 = 1








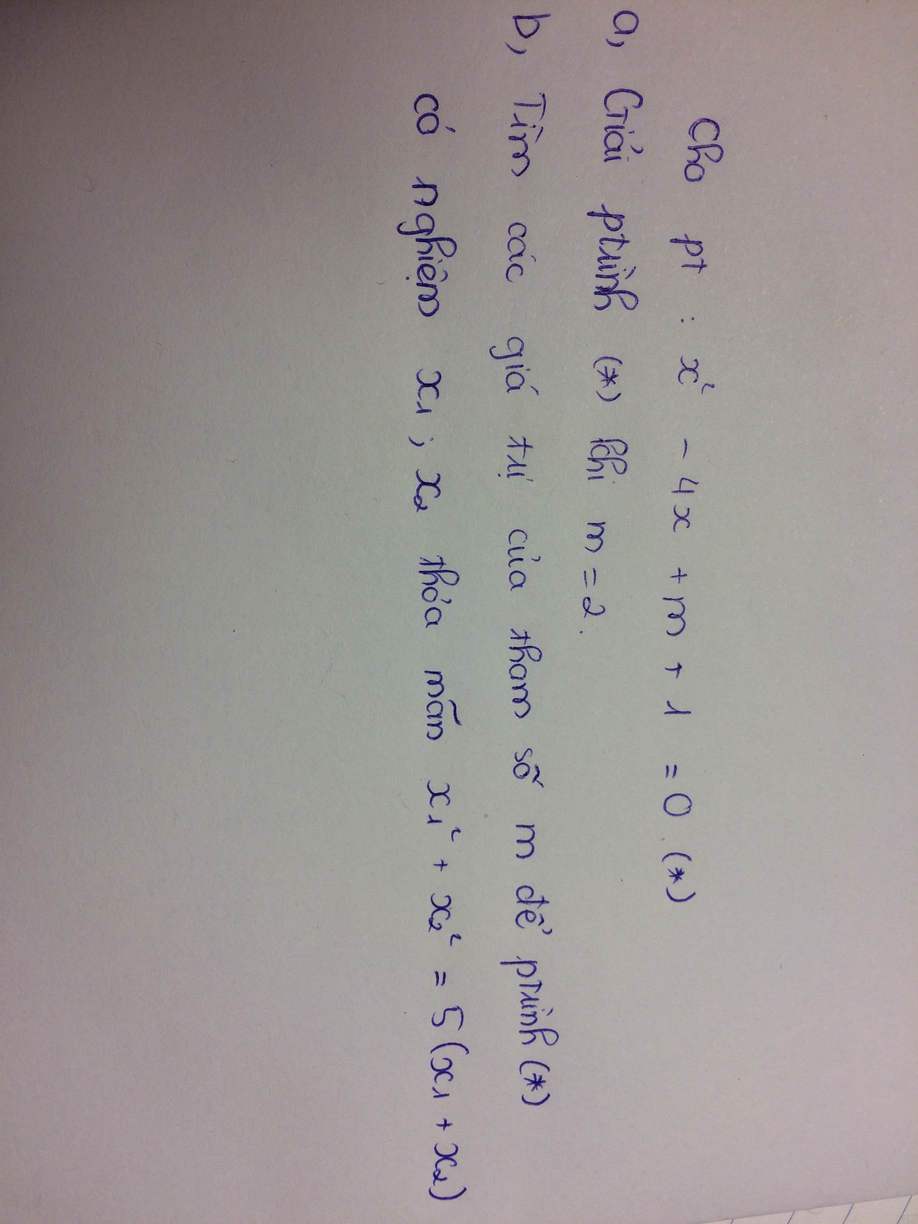


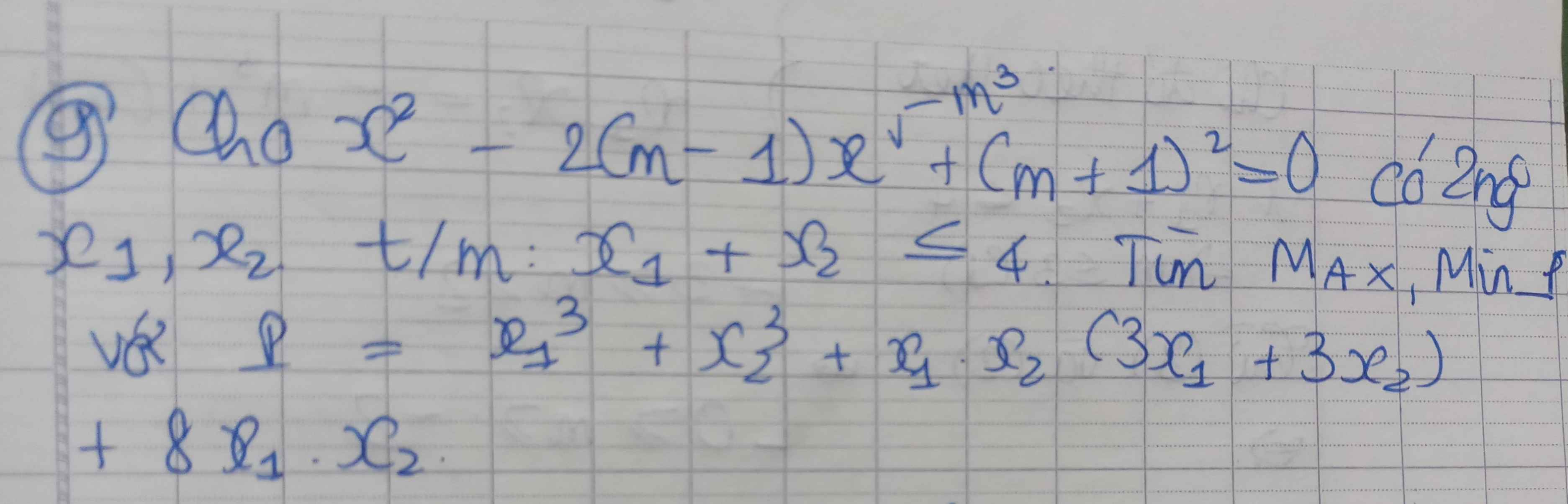

 e b
e b







