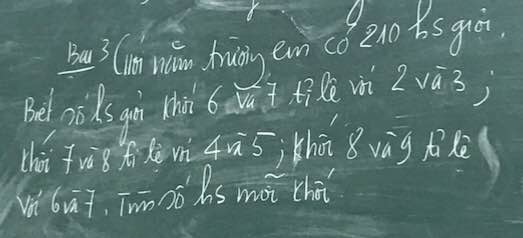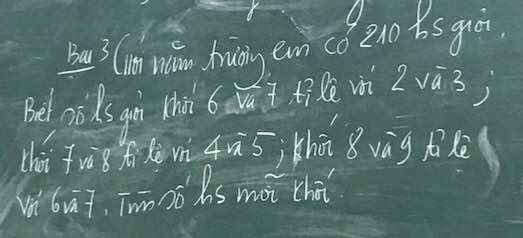\(a,Ta.có:\left|\dfrac{3}{5}-x\right|\ge0\forall x\)
\(\Rightarrow A=\left|\dfrac{3}{5}-x\right|+\dfrac{1}{9}\ge\dfrac{1}{9}\)
\(Dấu."=".xảy.ra.khi\\ \left|\dfrac{3}{5}-x\right|=0\\ \Rightarrow\dfrac{3}{5}-x=0\\ \Rightarrow x=0+\dfrac{3}{5}\\ \Rightarrow x=\dfrac{3}{5}\)
\(Vậy.Min.A=\dfrac{1}{9}\Leftrightarrow x=\dfrac{3}{5}\)
\(b,Ta.có:\\ \left(2x+1\right)^2\ge0\forall x\\ \Rightarrow-\left(2x+1\right)^2\le0\forall x\\ \Rightarrow B=-\left(2x+1\right)^2-5\le-5\forall x\\ Dấu."=".xảy.ra.khi:\\ -\left(2x+1\right)=0\\ \Rightarrow2x+1=0\\ \Rightarrow2x=0-1\\ 2x=-1\\ x=-1:2\\ x=-\dfrac{1}{2}\\ Vây.Max.A=-5\Leftrightarrow x=-\dfrac{1}{2}\)