3x - 2y = 5 ⇔ 6x - 4y = 10
và 2x + 3y = 12 ⇔ 6x + 9y = 36
⇔ 13y = 26
và 2x + 3y = 12
⇔ y = 2
và 2x + 3.2 = 12
⇔ y = 2
và 2x = 6
⇔ y = 2
và x = 3
Vậy S = {(3; 2)}
Bài 1:Giải hệ phương trình bằng phương pháp cộng đại số
\(\left\{{}\begin{matrix}17x+4y=2\\13x+2y=1\end{matrix}\right.\)
Bài 2:Giải bài toán sau bằng cách lập hệ phương trình
Hai người đi xe máy cùng khởi hành một lúc từ 2 địa điểm A và B cách nhau 180km,đi ngược chiều nhau và gặp nhau sau 2 giờ.Tính vận tốc của hai người đó biết rằng vận tốc của người đi từ A bằng vận tốc người đi từ B
Giải hệ phương trình sau (bằng cách cộng đại số):
3/ \(\left\{{}\begin{matrix}\dfrac{1}{x-2}+\dfrac{1}{y-1}=2\\\dfrac{2}{x-2}-\dfrac{3}{y-1}=1\end{matrix}\right.\)
Giải các phương trình sau theo phương pháp đặt ẩn phụ:
{\(\dfrac{5}{x+1}+\dfrac{1}{y-1}=10\)
\(\dfrac{1}{x-2}+\dfrac{3}{y-1}=18\)
Giải các phương trình sau theo phương pháp đặt ẩn phụ:
a.{\(\dfrac{12}{x-3}-\dfrac{5}{y+2}=63\)
\(\dfrac{8}{x-3}+\dfrac{15}{y+2}=-13\)
b.{\(4\sqrt{x+3}-9\sqrt{y+1}=2\)
\(5\sqrt{x+3}+3\sqrt{y+1}=31\)
Giải hệ pt = 2 phương pháp thế và cộng đại số
\(\left\{{}\begin{matrix}x-y=9\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{6}\end{matrix}\right.\)
Cho hệ phương trình: { 2mx + y = 2 (m mà than số)
{ 8x + my = m + 2
a) Giải hệ phương trình khi m = -1
b) Tìm m để hệ phương trình có nghiệm là x = 2; y = 6
c) Giải và biện luận hệ phương trình theo m
d) Trong trường hợp có nghiệm duy nhất:
+ Tìm hệ thức liên hệ giữa 2 nghiệm không phụ thuộc m
+ Tìm m để 4x + 3y = 7
+ Tìm m để x - y > 0
+ Tìm m để P = y^2 - 2x đạt giá trị nhỏ nhất
Giải hệ phương trình sau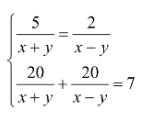
Cho phương trình x^2-2x+m=0(1)(m là tham số) a,giải phương trình (1) với m=-3 b,tìm m để phương trình 1 có 2 nghiệm x1x2 thoả mãn 1/x1^2 + 1/x2^2 =2
Giải hệ phương trình bằng phương pháp cộng đaị số:
\(\left\{{}\begin{matrix}\sqrt{5}x-\left(1+\sqrt{3}\right)y=1\\\left(1-\sqrt{3}\right)x+\sqrt{5}y=1\end{matrix}\right.\)
