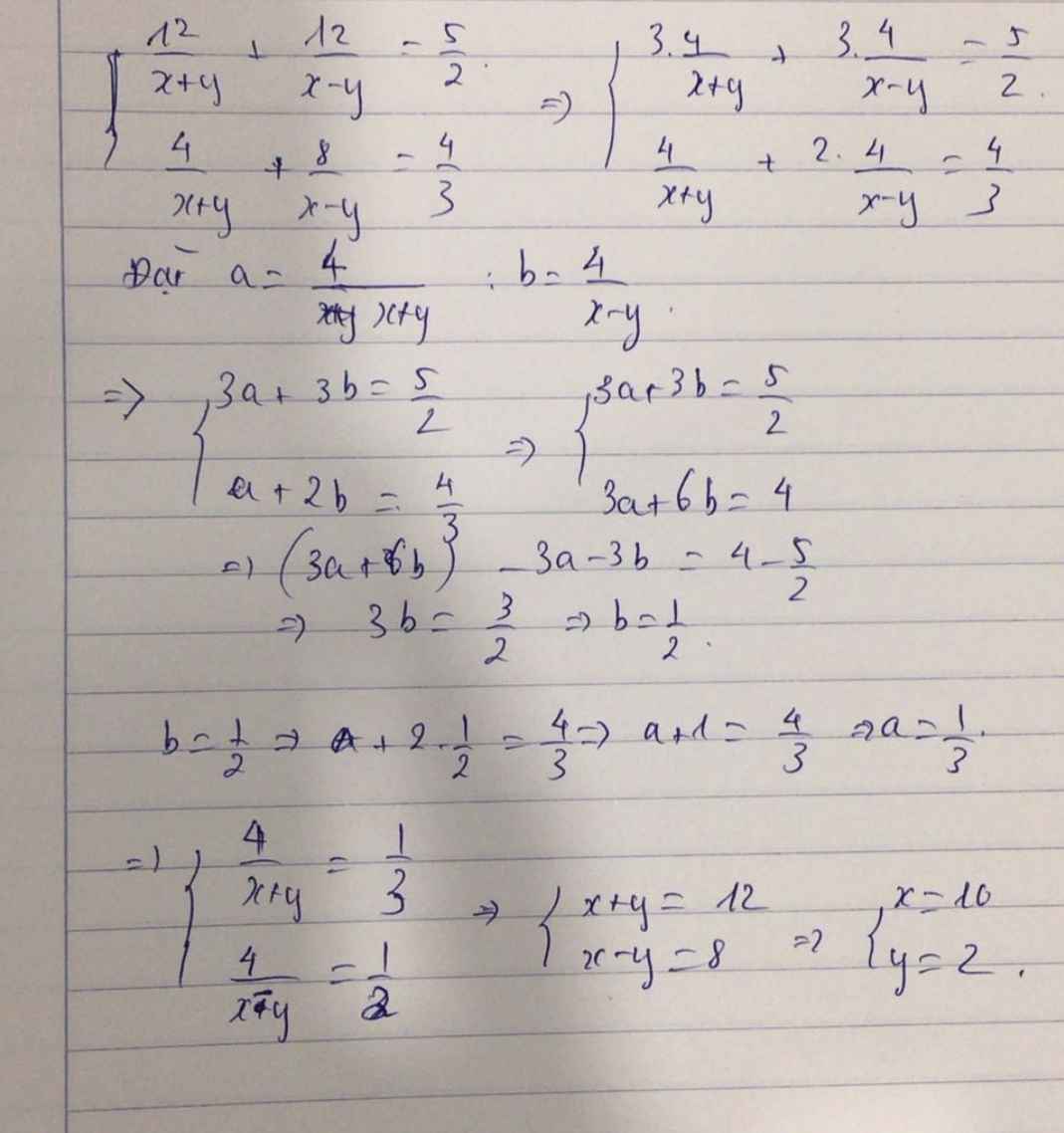\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3.4}{x+y}+\dfrac{3.4}{x-y}=\dfrac{5}{2}\\\dfrac{4}{x+y}+\dfrac{2.4}{x+y}=\dfrac{4}{3}\end{matrix}\right.\\ Đặt.a=\dfrac{4}{x+y},b=\dfrac{4}{x-y}\\ \Leftrightarrow\left\{{}\begin{matrix}3a+3b=\dfrac{5}{2}\\a+2b=\dfrac{4}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3a+3b=\dfrac{5}{2}\\3a+6b=4\end{matrix}\right.\)
\(\Leftrightarrow\left(3a+6b\right)-3a-3b=4-\dfrac{5}{2}\\ \Leftrightarrow3b=\dfrac{3}{2}\Rightarrow b=\dfrac{1}{2}\Rightarrow a+2.\dfrac{1}{2}=\dfrac{4}{3}\\\Leftrightarrow a+1=\dfrac{4}{3}\Rightarrow a=\dfrac{1}{3}\\ \Rightarrow\left\{{}\begin{matrix}\dfrac{4}{x+y}=\dfrac{1}{3}\\\dfrac{4}{x+y}=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+y=12\\x-y=8\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=10\\y=2\end{matrix}\right.\)