Bài 1: Phương trình bậc nhất hai ẩn

1. Khái niệm phương trình bậc nhất hai ẩn

- Phương trình bậc nhất hai ẩn \(x\) và \(y\) là hệ thức dạng: 

\(ax+by=c \qquad (1)\)

trong đó \(a,b,c\) là các số đã biết thỏa mãn \(a\ne0\) hoặc \(b\ne0\).

Ví dụ: \(2x+3y=1\), \(-\dfrac{1}{2}x+2y=-\dfrac{5}{3}\), \(3x+0y=-4\); \(0x-\sqrt{2}y=2\) là các phương trình bậc nhất hai ẩn.​

Nhận xét: Các hệ số \(a,b,c\) có thể là số nguyên, phân số, số thập phân, căn thức ..., có thể âm, dương hoặc bằng 0 nhưng phải đảm bảo điều kiện \(a\) và \(b\) không đồng thời bằng 0.

- Trong phương trình (1), nếu giá trị của vế trái tại \(x=x_0\) và \(y=y_0\) bằng vế phải thì cặp số \(\left(x_0;y_0\right)\) được gọi là một nghiệm của phương trình (1).

Ta cũng viết: Phương trình (1) có nghiệm \(\left(x;y\right)=\left(x_0;y_0\right)\).

Ví dụ: Cặp số \(\left(1;-2\right)\) là một nghiệm của phương trình \(3x-y=5\) vì \(3.1-\left(-2\right)=5\); nhưng \(\left(0;1\right)\) không là nghiệm của phương trình trên vì \(3.0-1=-1\ne5\).

Nhận xét:

+ Nghiệm của phương trình \(ax+by=c\) phải là một cặp số dạng \(\left(x_0;y_0\right)\). 

+ Kết luận "\(x_0\) và \(y_0\) là nghiệm của phương trình (1)" là kết luận sai.

- Trong mặt phẳng tọa độ, mỗi nghiệm của phương trình (1) được biểu diễn bởi một điểm. Nghiệm \(\left(x_0;y_0\right)\) được biểu diễn bởi điểm \(\left(x_0;y_0\right)\).

- Tập nghiệm của phương trình (1) là tập hợp các cặp số \(\left(x_0;y_0\right)\) là nghiệm của (1).

- Hai phương trình được gọi là tương đương nếu nó có cùng tập nghiệm.

- Ta có thể áp dụng quy tắc chuyển vế và quy tắc nhân để biến đổi phương trình bậc nhất hai ẩn.

2. Tập nghiệm của phương trình bậc nhất hai ẩn

Xét phương trình \(ax+by=c\qquad (1)\):

a) Nếu \(a\ne0\) và \(b\ne0\): 

\(\left(1\right)\Leftrightarrow y=-\dfrac{a}{b}x+\dfrac{c}{b}\). 

Như vậy, với mỗi giá trị \(x\) bất kì thì cặp số \(\left(x;y\right)\) với \(y=-\dfrac{a}{b}x+\dfrac{c}{b}\) là một nghiệm của (1).

Ta nói: Tập nghiệm của (1) là  \(S=\left\{\left(x;-\dfrac{a}{b}x+\dfrac{c}{b}\right):x\in R\right\}\).

Ta đã biết: đồ thị biểu diễn \(y=-\dfrac{a}{b}x+\dfrac{c}{b}\) là một đường thẳng 

\(\Rightarrow\) Tập nghiệm của (1) được biểu diễn bởi đường thẳng \(\left(d\right):ax+by=c\).

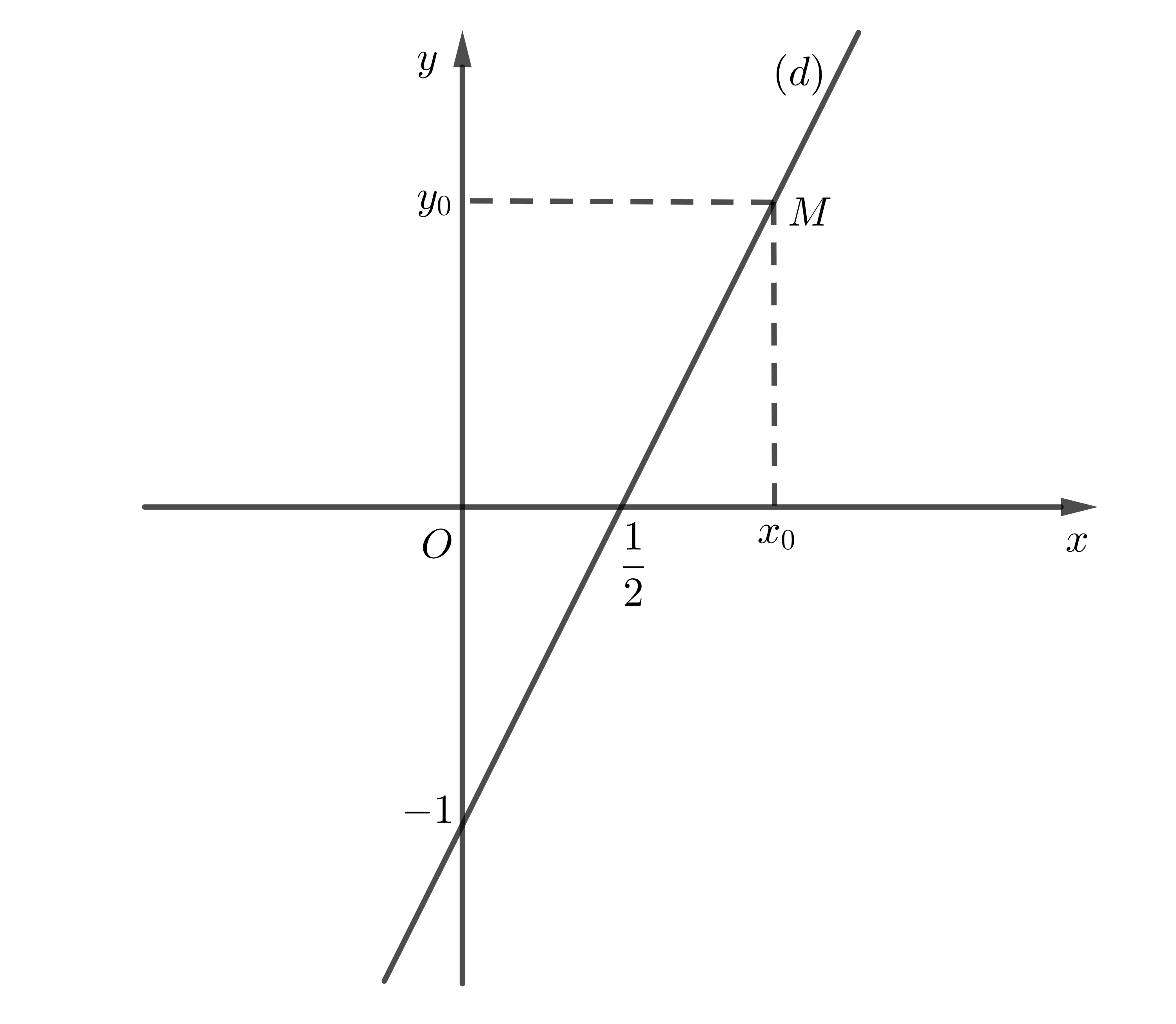
Ví dụ: Xét phương trình \(2x-y=1\)   (2)

Ta có: (2)\(\Leftrightarrow y=2x-1\) 

Vậy tập nghiệm của (2) là \(S=\left\{\left(x;2x-1\right):x\in R\right\}\). Tập nghiệm này được biểu diễn bởi đường thẳng \(\left(d\right):2x-y=1\) như sau:

b) Nếu \(a\ne0,b=0\): 

\(\left(1\right)\Leftrightarrow ax=c\Leftrightarrow x=\dfrac{c}{a}\)

Vậy tập nghiệm của (1) là \(S=\left\{\left(\dfrac{c}{a};y\right):y\in R\right\}\).

Tập nghiệm này được biểu diễn bởi đường thẳng \(\left(d\right):x=\dfrac{c}{a}\). Đường thẳng này đi qua điểm \(A\left(\dfrac{c}{a};0\right)\) và song song trục tung.

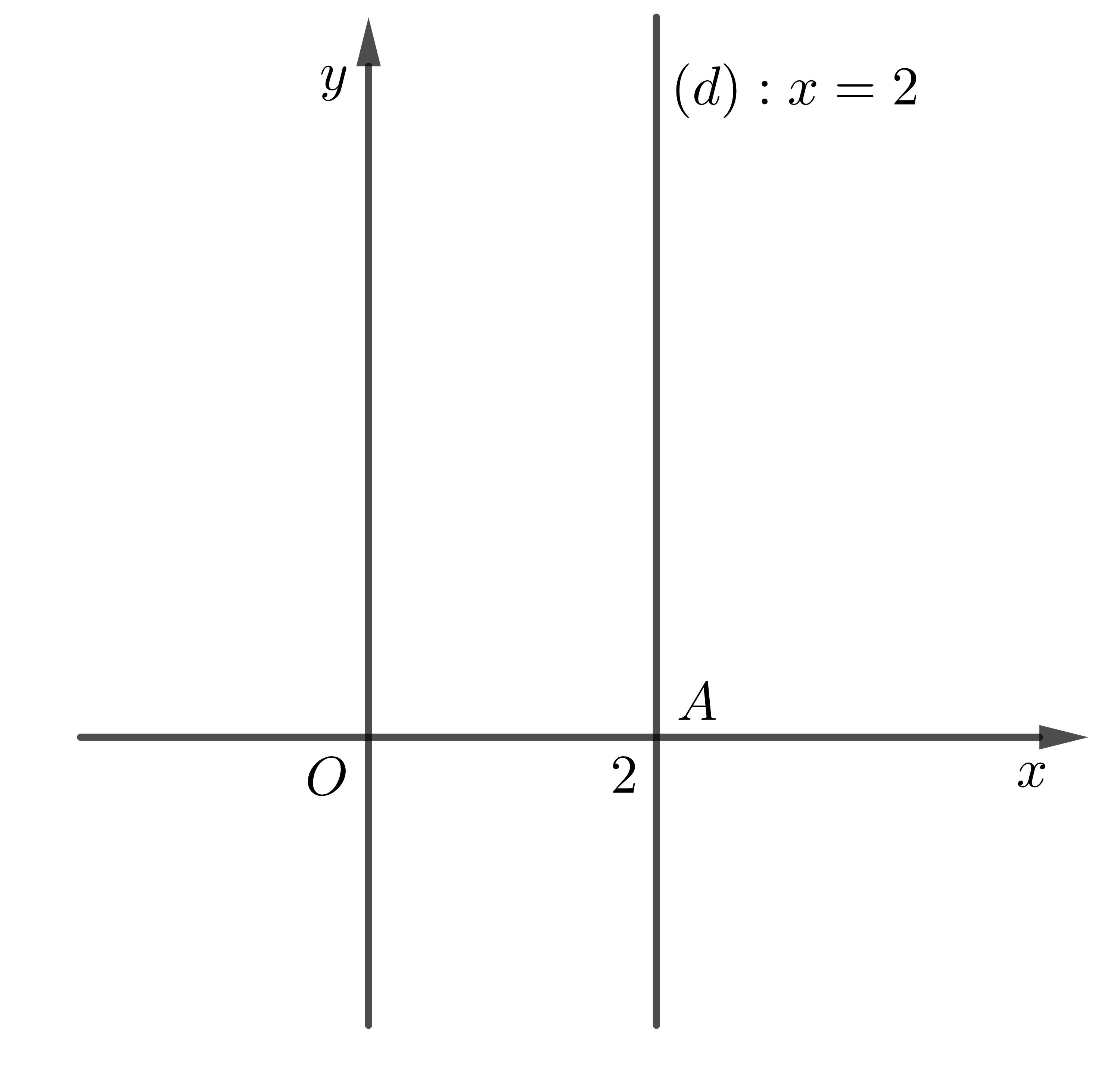
Ví dụ: Xét phương trình \(2x+0y=4\)   (3)

Ta có: \(\left(3\right)\Leftrightarrow x=2\) 

Tập nghiệm của (3) là \(S=\left\{\left(2;y\right):y\in R\right\}\). Tập nghiệm này được biểu diễn bởi đường thẳng \(\left(d\right):x=2\)

c) Nếu \(a=0,b\ne0\): 

\(\left(1\right)\Leftrightarrow by=c\Leftrightarrow y=\dfrac{c}{b}\)

Như vậy tập nghiệm của (1) là \(S=\left\{\left(x;\dfrac{c}{b}\right):x\in R\right\}\).

Tập nghiệm này được biểu diễn bởi đường thẳng \(\left(d\right):y=\dfrac{c}{b}\). Đây là đường thẳng đi qua \(B\left(0;\dfrac{c}{b}\right)\) và song song với trục hoành.

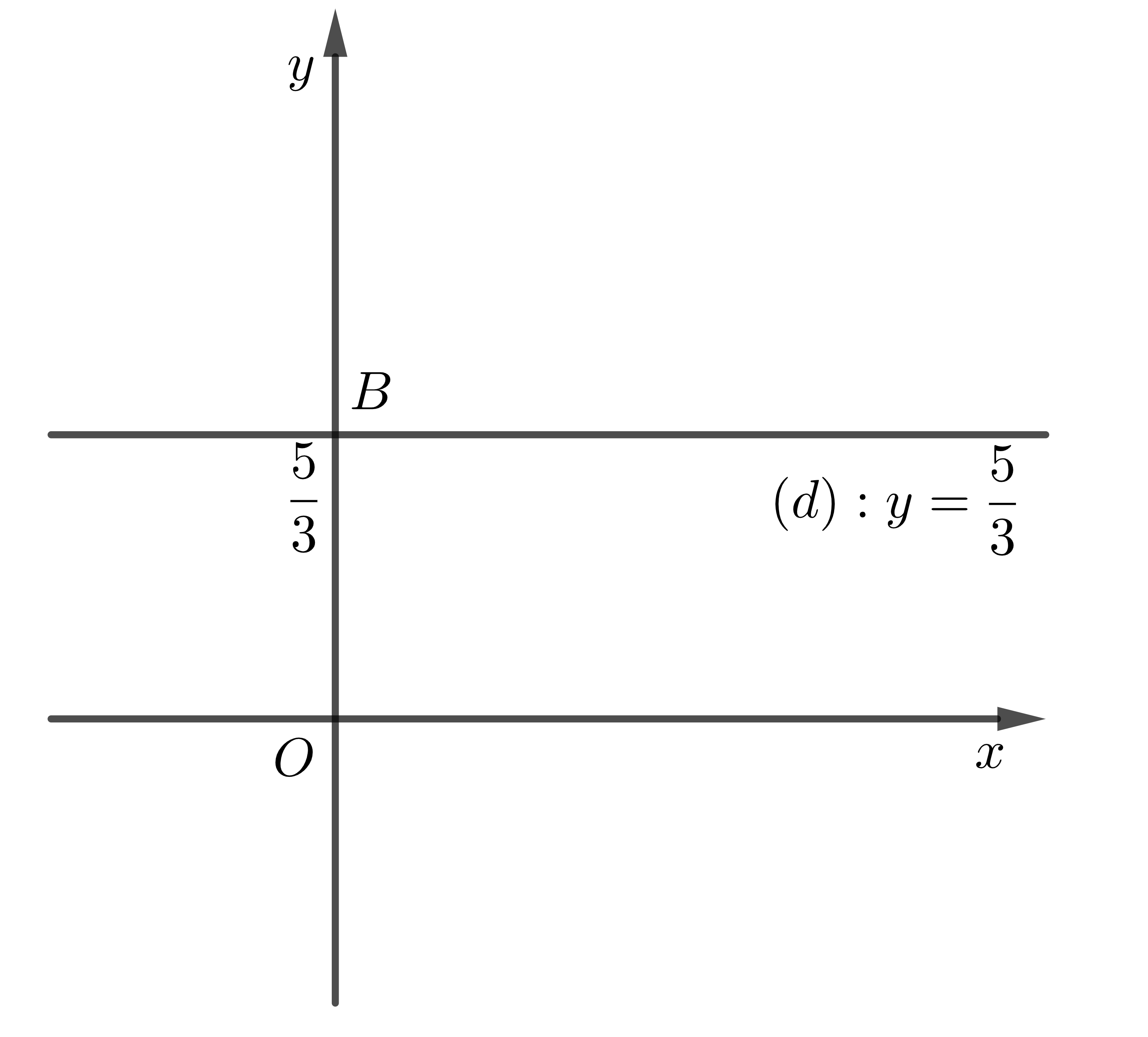
Ví dụ: Xét phương trình \(0x-3y=-5\)    (4)

Ta có (4) \(\Leftrightarrow y=\dfrac{5}{3}\)

Tập nghiệm của (4) là \(S=\left\{\left(x;\dfrac{5}{3}\right):x\in R\right\}\). Tập nghiệm này được biểu diễn bởi đường thẳng \(\left(d\right):y=\dfrac{5}{3}\)