a) Ta có: \(\dfrac{1}{2+\sqrt{3}}-\dfrac{2}{3+\sqrt{3}}+\dfrac{\sqrt{2}}{\sqrt{6}}\)
\(=\dfrac{2-\sqrt{3}}{1}-\dfrac{2\left(3-\sqrt{3}\right)}{6}+\dfrac{\sqrt{12}}{6}\)
\(=\dfrac{12-6\sqrt{3}-6+2\sqrt{3}+2\sqrt{3}}{6}\)
\(=\dfrac{6-2\sqrt{3}}{6}=\dfrac{3-\sqrt{3}}{3}\)
b) Ta có: \(\left(3-\dfrac{5-\sqrt{5}}{1-\sqrt{5}}\right)\left(\dfrac{\sqrt{10}+\sqrt{15}}{\sqrt{2}+\sqrt{3}}-3\right)\)
\(=\left(3+\dfrac{\sqrt{5}\left(1-\sqrt{5}\right)}{1-\sqrt{5}}\right)\left(\dfrac{\sqrt{5}\left(\sqrt{2}+\sqrt{3}\right)}{\sqrt{2}+\sqrt{3}}-3\right)\)
\(=\left(\sqrt{5}+3\right)\left(\sqrt{5}-3\right)\)
=5-9=-4
c) Ta có: \(\dfrac{12}{4-\sqrt{10}}-6\sqrt{\dfrac{5}{2}}+\dfrac{5\sqrt{2}+\sqrt{10}}{\sqrt{5}+1}\)
\(=\dfrac{12\left(4+\sqrt{10}\right)}{6}-6\cdot\dfrac{\sqrt{5}}{\sqrt{2}}+\dfrac{\sqrt{10}\left(\sqrt{5}+1\right)}{\sqrt{5}+1}\)
\(=2\left(4+\sqrt{10}\right)-3\sqrt{10}+\sqrt{10}\)
\(=8\)
d) Ta có: \(\sqrt[3]{\left(4+2\sqrt{3}\right)\left(\sqrt{3}+1\right)}\)
\(=\sqrt[3]{\left(\sqrt{3}+1\right)^3}\)
\(=\sqrt{3}+1\)
Bạn đã có hướng dẫn giải phía dưới sao còn cần giải giúp?

 giải giúp
giải giúp



 giải giúp
giải giúp giải giúp
giải giúp Giải giúp
Giải giúp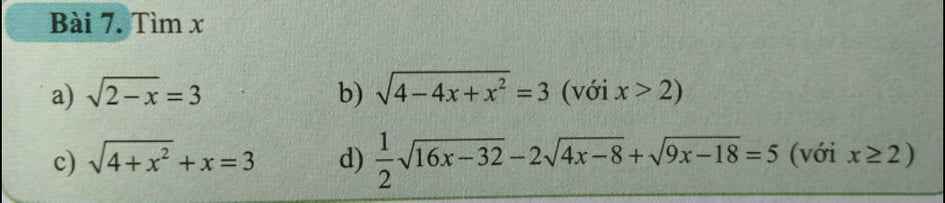 Giải giúp a b
Giải giúp a b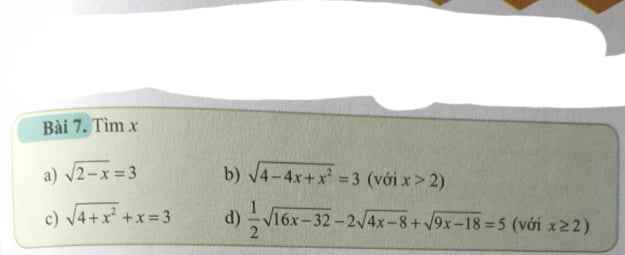 giải giúp c d
giải giúp c d giải giúp câu c
giải giúp câu c giải giúp a b
giải giúp a b

