Lời giải:
a. \(Q=\left(\frac{\sqrt{x}-(\sqrt{x}-1)}{\sqrt{x}(\sqrt{x}-1)}\right):\frac{(\sqrt{x}+1)(\sqrt{x}-1)-(\sqrt{x}+2)(\sqrt{x}-2)}{(\sqrt{x}-2)(\sqrt{x}-1)}\)
\(=\frac{1}{\sqrt{x}(\sqrt{x}-1)}:\frac{x-1-(x-4)}{(\sqrt{x}-2)(\sqrt{x}-1)}=\frac{1}{\sqrt{x}(\sqrt{x}-1)}.\frac{(\sqrt{x}-2)(\sqrt{x}-1)}{3}=\frac{\sqrt{x}-2}{3\sqrt{x}}\)
b. Để $Q$ nhận giá trị dương thì $\frac{\sqrt{x}-2}{3\sqrt{x}}>0$
$\Leftrightarrow \sqrt{x}-2>0\Leftrightarrow x>4$
Kết hợp với đkxđ suy ra $x>4$
Đúng 1
Bình luận (0)

 Giải giúp
Giải giúp

 giải giúp
giải giúp giải giúp
giải giúp giải giúp
giải giúp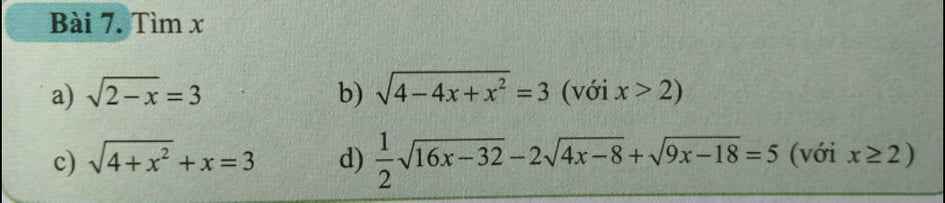 Giải giúp a b
Giải giúp a b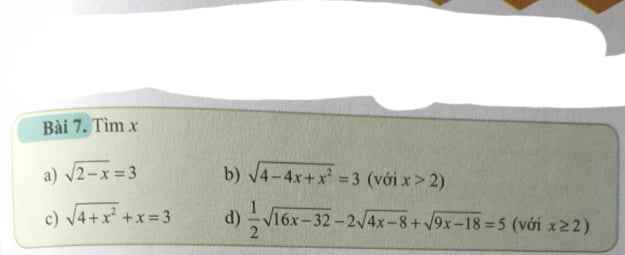 giải giúp c d
giải giúp c d giải giúp câu c
giải giúp câu c giải giúp a b
giải giúp a b

