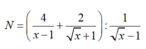a) \(\Leftrightarrow A=\dfrac{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}{\sqrt{x}\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}-\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(\Leftrightarrow A=\dfrac{x+2\sqrt{x}-3-x+2\sqrt{x}+3}{\sqrt{x}\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(\Leftrightarrow A=\dfrac{4\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}=\dfrac{4}{x-1}\)
b) \(A=7\) \(\Leftrightarrow\dfrac{4}{x-1}=7\)
\(\Leftrightarrow7x-7=4\) \(\Leftrightarrow7x=11\Leftrightarrow x=\dfrac{11}{7}\left(TM\right)\)
\(a,A=\dfrac{x+2\sqrt{x}-3-x+2\sqrt{x}+3}{\sqrt{x}\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}=\dfrac{4\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{4}{x-1}\\ b,A=7\Leftrightarrow x-1=\dfrac{4}{7}\Leftrightarrow x=\dfrac{11}{7}\left(tm\right)\)
\(a.A=\dfrac{\left(\sqrt{x}+3\right).\left(\sqrt{x}-1\right)-\left(\sqrt{x}-3\right).\left(\sqrt{x}+1\right)}{\sqrt{x}\left(x-1\right)}\)
\(=\dfrac{x-\sqrt{x}+3\sqrt{x}-3-x-\sqrt{x}+3\sqrt{x}+3}{\sqrt{x}\left(x-1\right)}\)
\(=\dfrac{\left(x-x\right)-\left(\sqrt{x}-3\sqrt{x}+\sqrt{x}-3\sqrt{x}\right)-\left(3-3\right)}{\sqrt{x}\left(x-1\right)}\)
\(=\dfrac{4\sqrt{x}}{\sqrt{x}\left(x-1\right)}=\dfrac{4}{x-1}\)
b. Để A=7 thì:
\(\dfrac{4}{x-1}=7< =>7x-7=4< =>7x=11< =>x=\dfrac{11}{7}\)