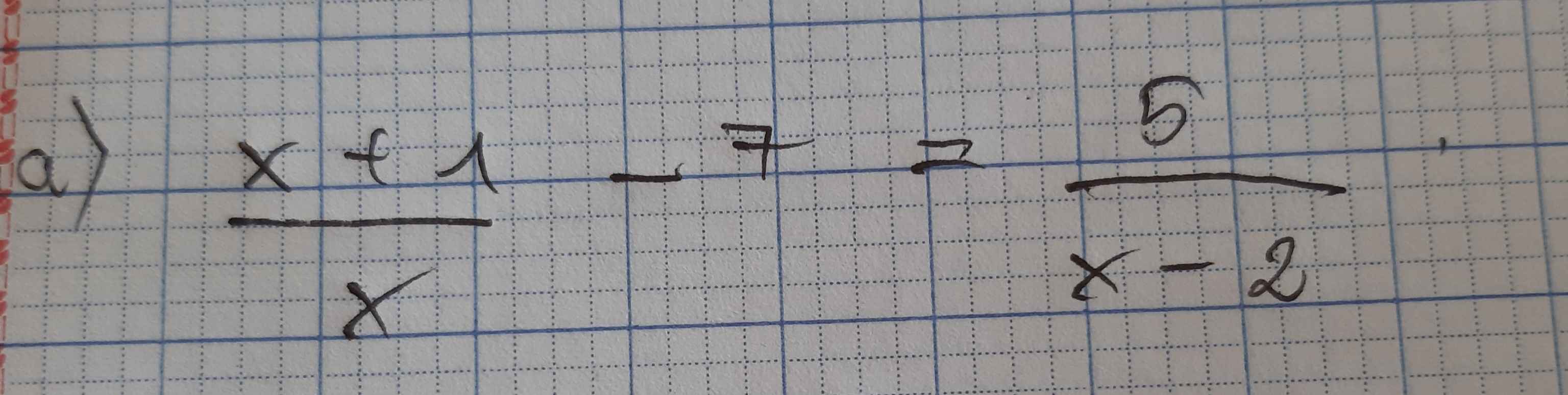\(\dfrac{x+1}{x}-7=\dfrac{5}{x-2}\)
\(ĐK:x\ne0;2\)
\(\Leftrightarrow\dfrac{\left(x+1\right)\left(x-2\right)-7x\left(x-2\right)}{x\left(x-2\right)}=\dfrac{5x}{x\left(x-2\right)}\)
\(\Leftrightarrow\left(x+1\right)\left(x-2\right)-7x\left(x-2\right)=5x\)
\(\Leftrightarrow x^2-2x+x-2-7x^2+14-5x=0\)
\(\Leftrightarrow-6x^2-6x+12=0\)
\(\Leftrightarrow-6\left(x^2+x+2\right)=0\)
Ta có: \(x^2+x+2>0;\forall x\)
Vậy pt vô nghiệm
Đúng 0
Bình luận (2)
