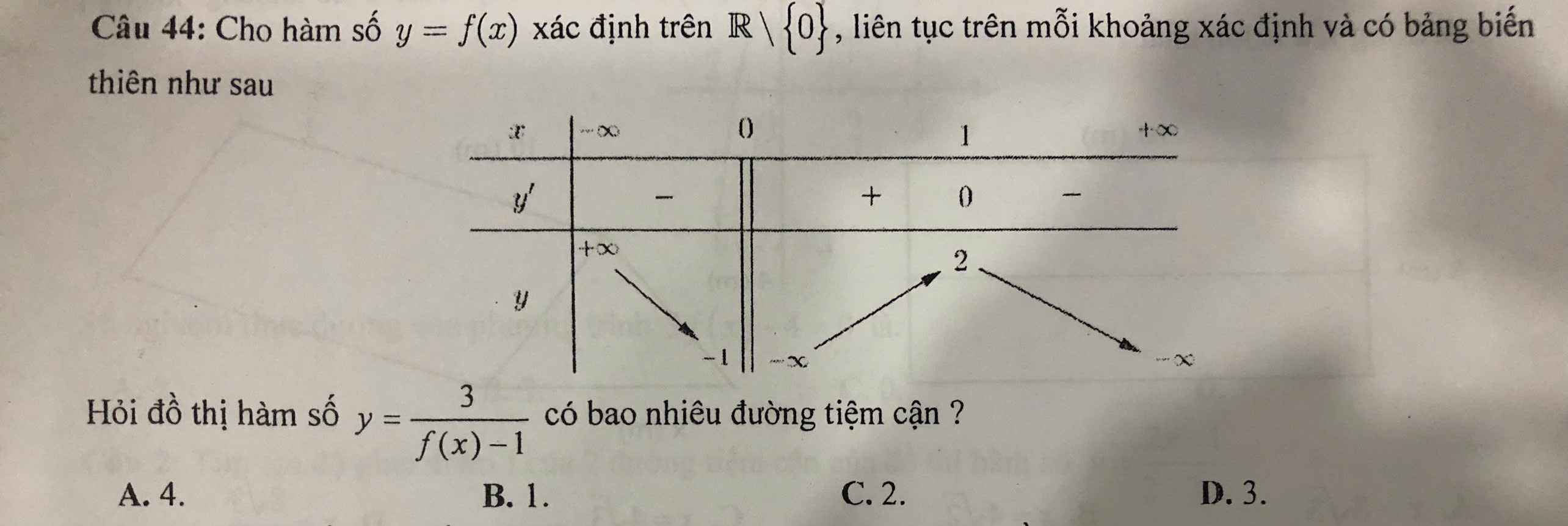
Dựa vào BBT ta thấy \(y=f\left(x\right)\) có 2 tiệm cận là \(TCĐ:x=0;TCN:y=-1\)
\(\Rightarrow f\left(x\right)-1\) có 2 tiệm cận \(x=0;y=-2\)
Nên \(f\left(x\right)\) là hàm phân thức cùng bậc ví dụ \(y=\dfrac{-2x+a}{x}\)
\(\Rightarrow y=\dfrac{3}{f\left(x\right)-1}\) cũng có 2 tiệm cận (TCĐ sẽ là \(x=\dfrac{a}{2}\) còn TCN là \(y=-\dfrac{3}{2}\))
Vậy chọn C
\(\lim\limits_{x\rightarrow\pm\infty}f\left(x\right)=\infty\) nên \(\lim\limits_{x\rightarrow\infty}\dfrac{3}{f\left(x\right)-1}=0\)
Do đó \(y=0\) là 1 TCN
Từ đồ thị ta thấy đường thẳng \(y=1\) cắt \(y=f\left(x\right)\) tại 3 điểm phân biệt
\(\Rightarrow f\left(x\right)-1=0\) có 3 nghiệm pb
\(\Rightarrow y=\dfrac{3}{f\left(x\right)-1}\) có 3 TCĐ
Vậy ĐTHS có tổng cộng 4 tiệm cận