a) 1,2x < -6 \(\Leftrightarrow\)x < -6 : 1,2 \(\Leftrightarrow\) x < - 5
Vậy tập nghiệm của bất phương trình là S = {x | x < -5}
b) 3x + 4 > 2x + 3
⇔ 3x - 2x > 3 - 4 \(\Leftrightarrow\) x > -1
Vậy tập nghiệm của bất phương trình là S = {x | x > -1}
Giải các bất phương trình và biểu diễn tập nghiệm trên trục số :
a) \(2x-3>0\)
b) \(3x+4< 0\)
c) \(4-3x\le0\)
d) \(5-2x\ge0\)
Giải các bất phương trình và biểu diễn tập nghiệm của chúng trên trục số :
a) \(2x-4< 0\)
b) \(3x+9>0\)
c) \(-x+3< 0\)
d) \(-3x+12>0\)
Giải các bất phương trình và biểu diễn tập nghiệm trên trục số :
a) \(\dfrac{15-6x}{3}>5\)
b) \(\dfrac{8-11x}{4}< 13\)
c) \(\dfrac{1}{4}\left(x-1\right)< \dfrac{x-4}{6}\)
d) \(\dfrac{2-x}{3}< \dfrac{3-2x}{5}\)
Giải bất phương trình sau và biểu diễn trên trục số 4x+7>23
giải bất phương trình và biểu diễn tập nghiệm:
c) 2x - 8 \(\ge\) 2\(\times\) ( x + 1/2)
d) \(\dfrac{5x^2-3x}{5}+\dfrac{3x+1}{4}< \dfrac{x\left(2x+1\right)}{2}-\dfrac{3}{2}\)
Giải các bất phương trình và biểu diễn tập nghiệm trên trục số:
1, 2(x-3)>_ 7-(x+2)
2, (x+2)•(x-3)<x(x-5)
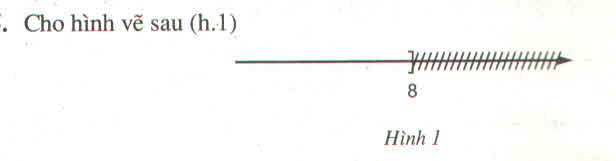
Bạn An cho rằng, hình vẽ đó biểu diễn tập nghiệm của bất phương trình \(2x\le16\), còn bạn Bình lại khẳng định hình vẽ đó là biểu diễn của tập nghiệm bất phương trình \(x+2\le10\)
Theo em bạn nào đúng ?
Hình vẽ sau biểu diễn tập nghiệm của bất phương trình nào ? (kể ba bất phương trình có cùng tập nghiệm)
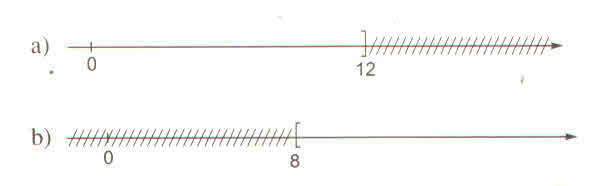
Giải các bất phương trình :
a) \(\dfrac{3x-1}{4}>2\)
b) \(\dfrac{2x+4}{3}< 3\)
c) \(\dfrac{1-2x}{3}>4\)
d) \(\dfrac{6-4x}{5}< 1\)
