4x+7>23
<=> 4x>16
<=>x> 4
Vậy tập nghiệm của bpt là{ x/x>4}
//////////////////|-----------)----------------->
0 4
Đúng 0
Bình luận (1)
Bài 4: Bất phương trình bậc nhất một ẩn.
Các câu hỏi tương tự
Giải các bất phương trình và biểu diễn tập nghiệm trên trục số :
a) \(1,2x< -6\)
b) \(3x+4>2x+3\)
Giải các bất phương trình và biểu diễn tập nghiệm trên trục số :
a) \(2x-3>0\)
b) \(3x+4< 0\)
c) \(4-3x\le0\)
d) \(5-2x\ge0\)
Giải các bất phương trình và biểu diễn tập nghiệm của chúng trên trục số :
a) \(2x-4< 0\)
b) \(3x+9>0\)
c) \(-x+3< 0\)
d) \(-3x+12>0\)
Giải các bất phương trình và biểu diễn tập nghiệm trên trục số:
1, 2(x-3)>_ 7-(x+2)
2, (x+2)•(x-3)<x(x-5)
Giải các bất phương trình và biểu diễn tập nghiệm trên trục số :
a) \(\dfrac{15-6x}{3}>5\)
b) \(\dfrac{8-11x}{4}< 13\)
c) \(\dfrac{1}{4}\left(x-1\right)< \dfrac{x-4}{6}\)
d) \(\dfrac{2-x}{3}< \dfrac{3-2x}{5}\)
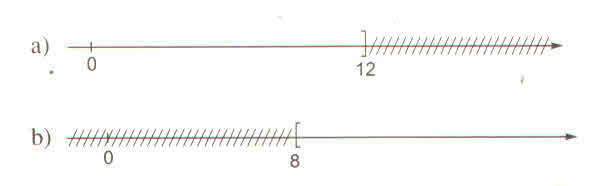
Hình vẽ sau biểu diễn tập nghiệm của bất phương trình nào ? (kể ba bất phương trình có cùng tập nghiệm)
Đố :
Tìm sai lầm trong các lời giải sau :
a) Giải bất phương trình -2x23. Ta có :
-2x23Leftrightarrow x23+2Leftrightarrow x25
Vậy nghiệm của bất phương trình là : x25
b) Giải bất phương trình -dfrac{3}{7}x12. Ta có :
-dfrac{3}{7}x12Leftrightarrowleft(-dfrac{7}{3}right).left(-dfrac{3}{4}xright)left(-dfrac{7}{3}right).12Leftrightarrow x-28
Vậy nghiệm của bất phương trình là x-28
Đọc tiếp
Đố :
Tìm sai lầm trong các "lời giải" sau :
a) Giải bất phương trình \(-2x>23\). Ta có :
\(-2x>23\Leftrightarrow x>23+2\Leftrightarrow x>25\)
Vậy nghiệm của bất phương trình là : \(x>25\)
b) Giải bất phương trình \(-\dfrac{3}{7}x>12\). Ta có :
\(-\dfrac{3}{7}x>12\Leftrightarrow\left(-\dfrac{7}{3}\right).\left(-\dfrac{3}{4}x\right)>\left(-\dfrac{7}{3}\right).12\Leftrightarrow x>-28\)
Vậy nghiệm của bất phương trình là \(x>-28\)
Giải bất phương trình sau :
a) 2x-7/x+3 >1
b) 4x+7/5-x >=0
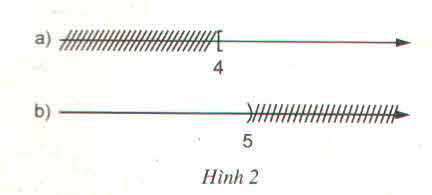
Viết bất phương trình bậc nhất một ẩn có tập nghiệm biểu diễn bởi hình vẽ sau (h.2)
